题目内容
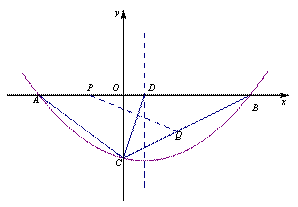
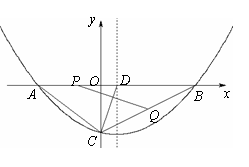
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.
 (1)求该抛物线的解析式;
(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;
 (3)在(2)的结论下,直线x=1上是否存在点M使,△MPQ为等腰三角形?若存在,请写出所有点M的坐标(请直接写出答案),若不存在,请说明理由.
(3)在(2)的结论下,直线x=1上是否存在点M使,△MPQ为等腰三角形?若存在,请写出所有点M的坐标(请直接写出答案),若不存在,请说明理由.
【提示:抛物线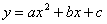 (
(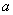 ≠0)的对称轴是
≠0)的对称轴是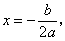 顶点坐标是
顶点坐标是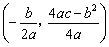 】
】
解:(1)∵抛物线过C(0,-6)
∴c=-6, 即y=ax2+bx-6…………………1分

…………………2分
解得:a= ,b=-
,b=-
∴该抛物线的解析式为 …………4分
…………4分
(2)存在…………………5分
设直线CD垂直平分PQ,
在Rt△AOC中,AC= =10=AD…………………6分
=10=AD…………………6分
∴点D在对称轴上,连结DQ 显然∠PDC=∠QDC,
由已知∠PDC=∠ACD,
∴∠QDC=∠ACD,
∴DQ∥AC, …………………7分
∴
∵AB=20,AD=10
∴DB=AB-AD=20-10=10=AD
∴
∴
∴DQ为△ABC的中位线,…………………8分
∴DQ= AC=5.
AC=5.
AP=AD-PD=AD-DQ=10-5=5
∴t=5÷1=5(秒) …………………9分
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,
在Rt△BOC中, BC= …………………10分
…………………10分
∴CQ=
∴点Q的运动速度为每秒 单位长度. …………………11分
单位长度. …………………11分
(本小题还可以连接DQ,PC,证明△APC≌△DQB,得到PA=PD=DQ,步骤参照上述标准给分)
(3)存在这样的五点:M1(1, -3), M2(1, ), M3(1,-
), M3(1,- ),
),
M4(1,  ),M5((1,
),M5((1,  )
)

为了解九年级学生的视力情况,某校随机抽取50名学生进行视力检查,结果如下:
| 视力 | 4.6以下 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.0以上 |
| 人数(人) | 6 | 15 | 5 | 10 | 3 | 4 | 7 |
这组数据的中位数是( ).
A.4.6 B.4.7 C.4.8 D.4.9

 的解集是 .
的解集是 .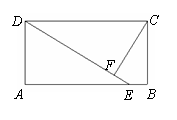 且DE=AB,过C作CF⊥DE于F.
且DE=AB,过C作CF⊥DE于F.  A.
A. B.
B. C.
C. D.
D.
 C. 0.010010001 D. π
C. 0.010010001 D. π ( )
( ) 时,发现 “( )”处的数字模糊不清,但察看答案可知解为
时,发现 “( )”处的数字模糊不清,但察看答案可知解为 则“( )”处的数字为 .
则“( )”处的数字为 .