题目内容

如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
（1）在图1中以格点为顶点画一个面积为5的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为3，4，5；
（3）在图3中以格点为顶点画一个三角形，使三角形三边长分别为2， $数学公式$ ， $数学公式$ ．

解：如图所示：

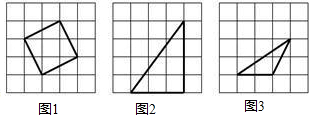
分析：（1）由正方形的面积为5，可知：正方形的变长为 $\text{[math]}$ ，1×2的长方形方格的对角线长是 $\text{[math]}$ ，从而作出面积为5的正方形；
（2）根据勾股定理可知：以3，4，5为三边所构成的三角形为直角三角形，故以3和4为两直角边作直角三角形即可；
（3）根据1×2的对角线为 $\text{[math]}$ ，3×2的对角线为 $\text{[math]}$ ，可作出变长为2， $\text{[math]}$ ， $\text{[math]}$ 的三角形．
点评：本题主要考查勾股定理在作图中的应用．

练习册系列答案

世纪金榜初中中考学业水平测试系列答案

智慧翔满格电课时作业本系列答案

考必胜3年中考2年模拟系列答案

寒假作业寒假快乐练西安出版社系列答案

贵州专版寒假作业吉林人民出版社系列答案

假期作业寒假成长乐园中国少年儿童出版社系列答案

优加学案中考真题详解汇编系列答案

同行课课100分过关作业系列答案

举一反三全能训练系列答案

快乐的假期生活寒假作业哈尔滨出版社系列答案

相关题目

如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画出图形．
（1）三边长分别为3，2

的三角形；
（2）一锐角为45°，面积为6的平行四边形；
（3）周长为20，面积为24的菱形．

18、如图，正方形网格中的每个小正方形边长都是1，每个小正方形的顶点叫做格点．
（1）请在图（1）中作一个格点钝角三角形；
（2）请在图（2）作一个四边长均为无理数且是轴对称图形的格点四边形．

如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．
（1）在图1中，画一个三角形，使它的三边长都是无理数；
（2）在图2中，画出一个直角三角形，使它的三边长都是整数；
（3）在图3中，画出一个中心对称图形．

（1）先化简，再求值：x（x-2）-（x+1）（x-1），其中x=10．
（2）已知x=

-1，求代数式（x+1）²-4（x+1）+4的值．
（3）如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫格点，请在给定的网格中按要求画图：
①从点A出发在图中画一条线段AB，使得AB=

；
②画出一个以（1）中的AB为斜边的等腰直角三角形，使三角形的三个顶点都在格点上，并根据所画图形求出等腰直角三角形的腰长．

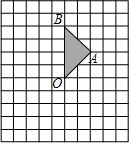如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABO的三个顶点A，B，O都在格点上．
（1）画出△ABO绕点O逆时针旋转90°后得到的三角形△A′B′O；
（2）根据所画的图找出A′点和B′点的坐标．