Question

【题目】设抛物线与x轴交于两个不同的点A（一1，0）、B（4，0），与y轴交于点C．

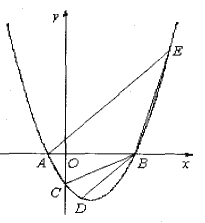
（1）求抛物线的解析式及∠ACB的度数；

（2）已知点D（1，n ）在抛物线上，过点A的直线交抛物线于另一点E．若点P在x轴上，以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标．

Answer 1

【答案】（1）、90°；（2）、，

【解析】

试题分析：（1）、首先求出函数解析式，根据相似和勾股定理得出∠ACB的度数；（2）、首先将点D的坐标代入二次函数解析式得出点D的坐标，然后过点E作EH⊥x轴于H，则H（6,0），然后分∽和∽两种情况分别求出点P的坐标.

试题解析：（1）、由题意得：

故抛物线的解析式为：

利用相似或勾股定理的逆定理易得

（2）、将D点坐标代入抛物线的解析式可得，从而D（1，-3）

可得方程组，

解之得或

故E（6，7）

过点E作EH⊥x轴于H，则H（6,0）

，

则点P只可能在点B的左侧，分两种情况讨论：

①若∽，可得

②若∽，可得

从而点P的坐标为，