��Ŀ����
��֪����ͼ1������E��0��-1����ƽ����x���ֱ��l��������y=| 1 |
| 4 |
��1�����A��B��F�����ꣻ
��2����֤��CF��DF��
��3����P��������y=
| 1 |
| 4 |
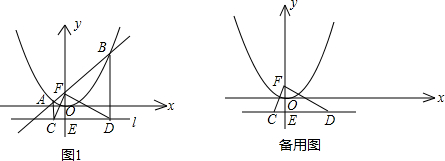
��������1�������ַ���������һ�Ǵ�ͳ�ĵ�Ĵ���ϵ��������������ͨ���������ߣ������BGF�ס�BHA�ɱ�����ϵ���F�����꣮
��2��Ҳ�����ַ���������һ����Rt��CEF�������DEF�߳����ù��ɶ���֤��CF��DF�����������ü��ι�ϵ�����CFD=90�㣻
��3������������⣬�ȼ�����ڣ����Ƿ��ҵ����������ĵ�P�����꣬����������������1��Rt��QPO��Rt��CFD����2��Rt��OPQ��Rt��CFD�����ݱ������P�����꣮
��2��Ҳ�����ַ���������һ����Rt��CEF�������DEF�߳����ù��ɶ���֤��CF��DF�����������ü��ι�ϵ�����CFD=90�㣻
��3������������⣬�ȼ�����ڣ����Ƿ��ҵ����������ĵ�P�����꣬����������������1��Rt��QPO��Rt��CFD����2��Rt��OPQ��Rt��CFD�����ݱ������P�����꣮
��� �⣺
�⣺
��1������һ����ͼ1����x=-1ʱ��y=
����x=4ʱ��y=4
��A��-1��
����1�֣�
B��4��4����2�֣�
��ֱ��AB�Ľ���ʽΪy=kx+b��3�֣�
��
���
��ֱ��AB�Ľ���ʽΪy=
x+1��4�֣�
��x=0ʱ��y=1��F��0��1����5�֣�
����������A��B��������ͬ����һ����ͼ2����FG��BD��AH��BD������ֱ�ΪG��H����y���ڵ�N �����ı�FOMG���ı���NOMH��Ϊ���Σ���FO=x��3�֣�
�����ı�FOMG���ı���NOMH��Ϊ���Σ���FO=x��3�֣�
�ߡ�BGF�ס�BHA
��
=
��
=
��4�֣�
���x=1
��F��0��1����5�֣�
��2��֤��������һ����Rt��CEF�У�CE=1��EF=2��
���ݹ��ɶ����ã�CF2=CE2+EF2=12+22=5��
��CF=
��6�֣�
��Rt��DEF��DE=4��EF=2
��DF2=DE2+EF2=42+22=20
��DF=2
�ɣ�1����C��-1��-1����D��4��-1��
��CD=5
��CD2=52=25
��CF2+DF2=CD2��7�֣�
���CFD=90��
��CF��DF��8�֣�
���������ɣ�1��֪AF=
=
��AC=
��AF=AC��6�֣�
ͬ����BF=BD
���ACF=��AFC
��AC��EF
���ACF=��CFO
���AFC=��CFO��7�֣�
ͬ������BFD=��OFD
���CFD=��OFC+��OFD=90��
��CF��DF��8�֣�
��3�����ڣ�
�⣺��ͼ3����PM��x�ᣬ����Ϊ��M��9�֣�
�֡�PQ��OP
��Rt��OPM��Rt��OQP
��
=
��
=
��10�֣�
��P��x��
x2����x��0����
��PM=
x2��OM=x
�ٵ�Rt��QPO��Rt��CFDʱ��
=
=
=
��11�֣�
��
=
=
���x=2��P1��2��1����12�֣�
�ڵ�Rt��OPQ��Rt��CFDʱ��
=
=
=2��13�֣�
��
=
=2
���x=8
��P2��8��16��
���ϣ����ڵ�P1��2��1����P2��8��16��ʹ�á�OPQ���CDF���ƣ���14�֣�
 �⣺
�⣺��1������һ����ͼ1����x=-1ʱ��y=
| 1 |
| 4 |
��A��-1��
| 1 |
| 4 |
B��4��4����2�֣�
��ֱ��AB�Ľ���ʽΪy=kx+b��3�֣�
��
|
���
|
��ֱ��AB�Ľ���ʽΪy=
| 3 |
| 4 |
��x=0ʱ��y=1��F��0��1����5�֣�
����������A��B��������ͬ����һ����ͼ2����FG��BD��AH��BD������ֱ�ΪG��H����y���ڵ�N
 �����ı�FOMG���ı���NOMH��Ϊ���Σ���FO=x��3�֣�
�����ı�FOMG���ı���NOMH��Ϊ���Σ���FO=x��3�֣��ߡ�BGF�ס�BHA
��
| BG |
| BH |
| FG |
| AH |
��
| 4-x | ||
4-
|
| 4 |
| 5 |
���x=1
��F��0��1����5�֣�
��2��֤��������һ����Rt��CEF�У�CE=1��EF=2��
���ݹ��ɶ����ã�CF2=CE2+EF2=12+22=5��
��CF=
| 5 |
��Rt��DEF��DE=4��EF=2
��DF2=DE2+EF2=42+22=20
��DF=2
| 5 |
�ɣ�1����C��-1��-1����D��4��-1��
��CD=5
��CD2=52=25
��CF2+DF2=CD2��7�֣�
���CFD=90��
��CF��DF��8�֣�
���������ɣ�1��֪AF=
1+(
|
| 5 |
| 4 |
| 5 |
| 4 |
��AF=AC��6�֣�
ͬ����BF=BD
���ACF=��AFC
��AC��EF
���ACF=��CFO
���AFC=��CFO��7�֣�
ͬ������BFD=��OFD
���CFD=��OFC+��OFD=90��
��CF��DF��8�֣�
��3�����ڣ�
�⣺��ͼ3����PM��x�ᣬ����Ϊ��M��9�֣�
�֡�PQ��OP
��Rt��OPM��Rt��OQP

��
| PM |
| PQ |
| OM |
| OP |
| PQ |
| OP |
| PM |
| OM |
��P��x��
| 1 |
| 4 |
��PM=
| 1 |
| 4 |
�ٵ�Rt��QPO��Rt��CFDʱ��
| PQ |
| OP |
| CF |
| DF |
| ||
2
|
| 1 |
| 2 |
��
| PM |
| OM |
| ||
| x |
| 1 |
| 2 |
���x=2��P1��2��1����12�֣�
�ڵ�Rt��OPQ��Rt��CFDʱ��
| PQ |
| OP |
| DF |
| CF |
2
| ||
|
��
| PM |
| OM |
| ||
| x |
���x=8
��P2��8��16��
���ϣ����ڵ�P1��2��1����P2��8��16��ʹ�á�OPQ���CDF���ƣ���14�֣�
������������һ���ۺ��Խ�ǿ���⣬ǰ���ʷ����࣬����ͨ�ķ�������ӱ�ķ����������ʵĸ����ߺ���Ҫ�����һ����̽�������⣬��ɢ˼ά��

��ϰ��ϵ�д�
�����Ŀ
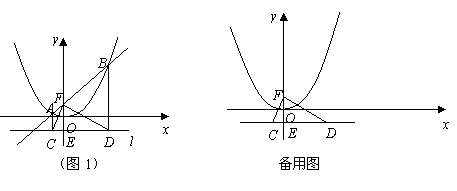

 x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF��
x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF�� x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ�á�OPQ���CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ�á�OPQ���CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
 x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF��
x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF�� x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ�á�OPQ���CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ�á�OPQ���CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�