题目内容
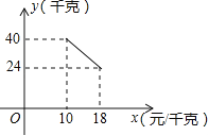
【题目】某经销商销售一种产品，这种产品的成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）该经销商想要每天获得150元的销售利润，销售价应定为多少？
【答案】（1）y=﹣2x+60（10≤x≤18）；（2）15.
【解析】
（1）设函数关系式y=kx+b，把（10，40），（18，24）代入求出k和b即可，由成本价为10元/千克，销售价不高于18元/千克，得出自变量x的取值范围；
（2）根据销售利润=销售量×每一件的销售利润与x的关系，利润为150建立等式，解一元二次方程求出x，再根据x的取值范围即可确定x的值．
解：（1）设y与x之间的函数关系式y=kx+b，把（10，40），（18，24）代入得
，
解得
，
∴y与x之间的函数关系式y=﹣2x+60（10≤x≤18）；
（2）（x﹣10）（﹣2x+60）=150，
解得
，
（不合题意，舍去）
答：该经销商想要每天获得150元的销售利润，销售价应定为15元．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
