题目内容
设A、B两点的坐标分别为（1，1）和（4，3），P点是x轴上的点，则PA+PB的最小值是________．
5
分析：先画出图形，由两点之间线段最短可知，作出A点对称点，当P点在线段AB上时PA+PB的值最小，即PA+PB=A′B，利用勾股定理求解即可．
解答：
解：作点A关于x轴的对称点A'，则A′坐标为（1，-1），
连接A′B交x轴于一点，此点就是点P，此时PA+PB最小，
作BE⊥y于一点E，延长A′A交BE于一点M，
∵PB=PA′，
∴PA+PB=BA′，
∵A、B两点的坐标分别为（1，1）和（4，3），A′坐标为（1，-1），
∴BM=4-1=3，MA′=1+3=4，
∴BA′=
=
=5．
∴PA+PB的最小值是5．
故答案为：5．
点评：此题主要考查了线路最短问题，解答此题的关键是画出图形，利用数形结合及勾股定理求解．
分析：先画出图形，由两点之间线段最短可知，作出A点对称点，当P点在线段AB上时PA+PB的值最小，即PA+PB=A′B，利用勾股定理求解即可．
解答：
解：作点A关于x轴的对称点A'，则A′坐标为（1，-1），连接A′B交x轴于一点，此点就是点P，此时PA+PB最小，
作BE⊥y于一点E，延长A′A交BE于一点M，
∵PB=PA′，
∴PA+PB=BA′，
∵A、B两点的坐标分别为（1，1）和（4，3），A′坐标为（1，-1），
∴BM=4-1=3，MA′=1+3=4，
∴BA′=
==5．∴PA+PB的最小值是5．
故答案为：5．
点评：此题主要考查了线路最短问题，解答此题的关键是画出图形，利用数形结合及勾股定理求解．
练习册系列答案
相关题目
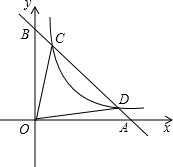于A、B两点，设C、D的坐标分别是（x1，y1）、（x2，y2），连接OC、OD．
y轴的负半轴上，且∠ACB=90°
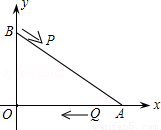
m2-mb+n），其中 a，b，c，m，n为实数，且a，m不为0．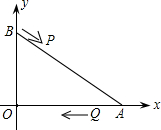
（2012•衡阳）如图，A、B两点的坐标分别是（8，0）、（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为t（0＜t＜
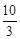）秒．解答如下问题：