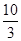题目内容
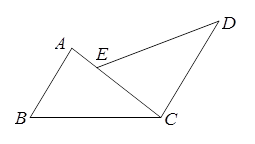
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(1)求证:DP平分∠ADC;
(2)若∠CEF=75°,CF=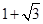 ,求△AEF的面积.
,求△AEF的面积.
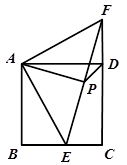
(1)求证:DP平分∠ADC;
(2)若∠CEF=75°,CF=
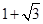 ,求△AEF的面积.
,求△AEF的面积.
(1)证明见解析;(2)2.
试题分析:(1)连接PC.根据直角三角形的性质可得PC=
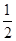 EF=PA.运用“SSS”证明△APD≌△CPD,得∠ADP=∠CDP;
EF=PA.运用“SSS”证明△APD≌△CPD,得∠ADP=∠CDP;(2)作PH⊥CF于H点.分别求DF和PH的长,再计算面积.设DF=x,在Rt△EFC中,∠CEF=60°,运用勾股定理可求DF;根据三角形中位线定理求PH.
试题解析:(1)证明:连接PC.
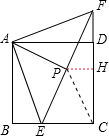
∵ABCD是正方形,
∴∠ABE=∠ADF=90°,AB=AD.
∵BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,AE=AF.
∴∠EAF=∠BAD=90°.
∵P是EF的中点,
∴PA=
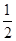 EF,PC=
EF,PC=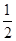 EF,
EF,∴PA=PC.
又∵AD=CD,PD=PD(公共边),
∴△PAD≌△PCD,(SSS)
∴∠ADP=∠CDP,即DP平分∠ADC;
(2)由(1)知△EAF是等腰直角三角形,
∴∠AEF=45°,
∴∠AEB=180°﹣45°﹣75°=60°,
∵设BE=x.
∴
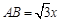 ,
,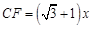 .
.又
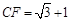 ,
,则
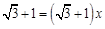 .
.解之,得
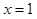
∴
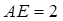
∴
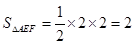

练习册系列答案
相关题目
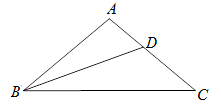
 的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.
的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.