题目内容
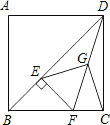 已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.求证:EG=CG.
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.求证:EG=CG.
分析:根据直角三角形斜边上的中线等于斜边的一半,EG=
DF,CG=
DF,所以EG=CG.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵EF⊥BD,
∴△DEF为直角三角形,
∵G为DF中点,
∴EG=
DF,(直角三角形斜边上的中线等于斜边的一半),
在正方形ABCD中,∠BCD=90°,
又G为DF中点,
∴CG=
DF,(直角三角形斜边上的中线等于斜边的一半),
∴EG=CG.
∴△DEF为直角三角形,
∵G为DF中点,
∴EG=
| 1 |
| 2 |
在正方形ABCD中,∠BCD=90°,
又G为DF中点,
∴CG=
| 1 |
| 2 |
∴EG=CG.
点评:本题主要考查直角三角形斜边上的中线等于斜边的一半的性质,熟练掌握性质是解题的关键.

练习册系列答案
相关题目
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.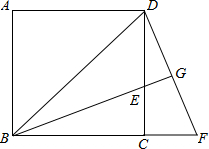 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.