题目内容
(2013•苏州一模)如图(1),在Rt△AOB中,∠AOB=90°,∠B=30°且AO=1,延长BA、BO,点C为BA延长线上的一动点,以每秒1个单位长度的速度从点A开始沿射线BA向上移动,作等边△CDE,点D和点E都在射线BO上,
(1)求BO的长;
(2)若半径为2
的⊙M与射线BO、射线BA相切于点G、F,求当等边△CDE的边CE与⊙M相切时的边长;
(3)以O为坐标原点,直线OB、OA为x轴、y轴建立如图(2)所示的直角坐标系,若以点C为顶点的抛物线y=a(x-m)2+n经过点E.⊙M与x轴、射线BA都相切,其半径为3(1-
)a.问点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?
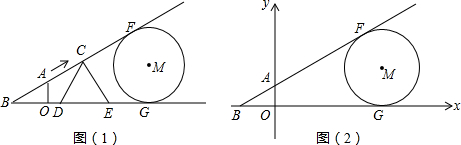
(1)求BO的长;
(2)若半径为2
| 3 |
(3)以O为坐标原点,直线OB、OA为x轴、y轴建立如图(2)所示的直角坐标系,若以点C为顶点的抛物线y=a(x-m)2+n经过点E.⊙M与x轴、射线BA都相切,其半径为3(1-
| 3 |
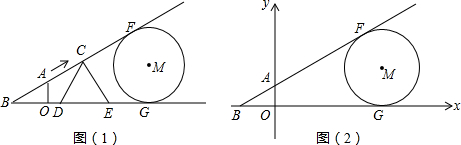
分析:(1)通过解Rt△AOB可以求得线段BO的长度
(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
(3)此题需要结合图形来解,首先画出第一次相切时的示意图(详见解答图);已知的条件只有圆的半径,那么先连接圆心与三个切点以及点E,首先能判断出四边形CPMN是正方形,那么CP与⊙M的半径相等,只要再求出PE就能进一步求得C点坐标;那么可以从PE=EQ,即Rt△MEP入手,首先∠CED=60°,而∠MEP=∠MEQ,易求得这两个角的度数,通过解直角三角形不难得到PE的长,即可求出PE及点C、E的坐标.然后利用C、E的坐标确定a的值,进而可求出AC的长,由此得解.
(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
(3)此题需要结合图形来解,首先画出第一次相切时的示意图(详见解答图);已知的条件只有圆的半径,那么先连接圆心与三个切点以及点E,首先能判断出四边形CPMN是正方形,那么CP与⊙M的半径相等,只要再求出PE就能进一步求得C点坐标;那么可以从PE=EQ,即Rt△MEP入手,首先∠CED=60°,而∠MEP=∠MEQ,易求得这两个角的度数,通过解直角三角形不难得到PE的长,即可求出PE及点C、E的坐标.然后利用C、E的坐标确定a的值,进而可求出AC的长,由此得解.
解答: 解:(1)∵在Rt△AOB中,∠AOB=90°,∠B=30°且AO=1,
解:(1)∵在Rt△AOB中,∠AOB=90°,∠B=30°且AO=1,
∴tan∠ABO=
=
,
∴BO=
;
(2)①如图(1)a,当CE在⊙M左侧相切于点H,连接MF、MG、MH,
∵AB、CE、BO均为⊙M的切线,
∴MF⊥AB,MH⊥CE,MG⊥BO,
∵∠ABO=30°,△CDE是等边三角形,
∴∠BCE=90°,
∴四边形CHMF为矩形,
∵MF=MH,
∴四边形CHMF为正方形,
∴CH=MH=2
,
∵EH、EG为⊙M的切线,∠CED=60°,
∴∠HEM=60°,
∴HE=
MH=2,
∵CE=CH+HE=2
+2;
②如图(1)b,当CE在⊙M右侧相切于点H,
由①证得:CH=MH=2
,
∵∠HEM=30°,
∴HE=
MH=6,
∴CE=CH+HE=2
+6;
(3)如图(2),设切点分别是Q,N,P,连接MQ,MN,MP,ME,过点C作CH⊥x轴,H为垂足,过A作AF⊥CH,F为垂足.
∵△CDE是等边三角形,∠ABO=30°
∴∠BCE=90°,∠ECN=90°
∵CE,直线AB分别与⊙M相切,
∴∠MPC=∠CNM=90°,
∴四边形MPCN为矩形,
∵MP=MN
∴四边形MPCN为正方形
∴MP=MN=CP=CN=3(1-
)a(a<0).
∵EC和x轴都与⊙M相切,
∴EP=EQ.
∵∠NBQ+∠NMQ=180°,
∴∠PMQ=60°
∴∠EMQ=30°,
∴在Rt△MEP中,tan30°=
,∴PE=(
-3)a
∴CE=CP+PE=3(1-
)a+(
-3)a=-2
a
∴DH=HE=-
a,CH=-3a,BH=-3
a,
∴OH=-3
a-
,OE=-4
a-
,
∴E(-4
a-
,0)
∴C(-3
a-
,-3a)
设二次函数的解析式为:y=a(x+3
a+
)2-3a
∵点E在该抛物线上
∴a(-4
a-
+3
a+
)2-3a=0
得:a2=1,解之得a1=1,a2=-1
∵a<0,∴a=-1
∴AF=2
,CF=2,∴AC=4
∴点C移动到4秒时,等边△CDE的边CE第一次与⊙M相切.
 解:(1)∵在Rt△AOB中,∠AOB=90°,∠B=30°且AO=1,
解:(1)∵在Rt△AOB中,∠AOB=90°,∠B=30°且AO=1,∴tan∠ABO=
| OA |
| OB |
| ||
| 3 |
∴BO=
| 3 |
(2)①如图(1)a,当CE在⊙M左侧相切于点H,连接MF、MG、MH,
∵AB、CE、BO均为⊙M的切线,
∴MF⊥AB,MH⊥CE,MG⊥BO,
∵∠ABO=30°,△CDE是等边三角形,
∴∠BCE=90°,
∴四边形CHMF为矩形,
∵MF=MH,
∴四边形CHMF为正方形,

∴CH=MH=2
| 3 |
∵EH、EG为⊙M的切线,∠CED=60°,
∴∠HEM=60°,
∴HE=
| 1 | ||
|
∵CE=CH+HE=2
| 3 |
②如图(1)b,当CE在⊙M右侧相切于点H,
由①证得:CH=MH=2
| 3 |
∵∠HEM=30°,
∴HE=
| 3 |
∴CE=CH+HE=2
| 3 |
(3)如图(2),设切点分别是Q,N,P,连接MQ,MN,MP,ME,过点C作CH⊥x轴,H为垂足,过A作AF⊥CH,F为垂足.
∵△CDE是等边三角形,∠ABO=30°
∴∠BCE=90°,∠ECN=90°
∵CE,直线AB分别与⊙M相切,
∴∠MPC=∠CNM=90°,
∴四边形MPCN为矩形,
∵MP=MN
∴四边形MPCN为正方形
∴MP=MN=CP=CN=3(1-
| 3 |
∵EC和x轴都与⊙M相切,
∴EP=EQ.
∵∠NBQ+∠NMQ=180°,
∴∠PMQ=60°
∴∠EMQ=30°,
∴在Rt△MEP中,tan30°=
| PE |
| PM |
| 3 |
∴CE=CP+PE=3(1-
| 3 |
| 3 |
| 3 |
∴DH=HE=-
| 3 |
| 3 |
∴OH=-3
| 3 |
| 3 |
| 3 |
| 3 |

∴E(-4
| 3 |
| 3 |
∴C(-3
| 3 |
| 3 |
设二次函数的解析式为:y=a(x+3
| 3 |
| 3 |
∵点E在该抛物线上
∴a(-4
| 3 |
| 3 |
| 3 |
| 3 |
得:a2=1,解之得a1=1,a2=-1
∵a<0,∴a=-1
∴AF=2
| 3 |
∴点C移动到4秒时,等边△CDE的边CE第一次与⊙M相切.
点评:本题考查了圆的综合,涉及了切线的性质、等边三角形的性质、特殊角的三角函数值解答本题的关键是数形结合思想及分类讨论思想的综合运用.难度在于涉及到动点问题,许多数值都不是具体值;(3)题中,正确画出草图、贯彻数形结合的解题思想是关键.

练习册系列答案
相关题目
 (2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(-
(2013•苏州一模)如图,在平面直角坐标系中,点D为y轴上一点,⊙D与坐标轴分别相交于A(- (2013•苏州一模)如图,正方形ABCD中,BE=CF.
(2013•苏州一模)如图,正方形ABCD中,BE=CF.