题目内容
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( )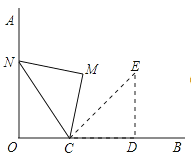
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,
∴∠ECN=75°,∵∠ECD=45°,∴∠NCO=180°-75°-45°=60°,
∵AO⊥OB,∴∠AOB=90°,∴∠ONC=30°,
设OC= ![]() ,则CN=2
,则CN=2 ![]() ,
,
∵等腰直角三角形DCE旋转到△CMN,
∴△CMN也是等腰直角三角形,
设CM=MN= ![]() ,则由勾股定理得:
,则由勾股定理得: ![]() 2+
2+ ![]() 2=(2
2=(2 ![]() )2 ,
)2 , ![]() =
= ![]() 即CD=CM=
即CD=CM= ![]() ∴
∴ ![]() =
= ![]() 故选C.
故选C.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目