Question

我们知道在三角形每一个顶点处各取一个外角，它们的和就是这个三角形的外角和．

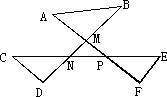
(1)如图，求出△MNP的外角和，并证明你的结论；

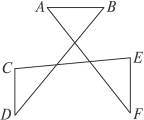
(2)猜想∠A、∠B、∠C、∠D、∠E、∠F的和是多少；

(3)请用(1)的结论证明(2)的猜想．

Answer 1

答案：
解析：

解：(1)△MNP的外角和等于360°．证明略． 　　(2)猜想：∠A、∠B、∠C、∠D、∠E、∠F的和为360°． 　　(3)证明：因为∠PMB＝∠A＋∠B，∠MNC＝∠C＋∠D，∠MPE＝∠E＋∠F， 　　所以∠A＋∠B＋∠C＋∠D＋∠E＋∠F 　　＝∠PMB＋∠MNC＋∠MPE＝360°．