题目内容
如图，圆形转盘中，A，B，C三个扇形区域的圆心角分别为150°，120°和90°．转动圆盘后，指针停止在任何位置的可能性都相同（若指针停在分界线上，则重新转动圆盘），则转动圆盘一次，指针停在B区域的概率是 ．
．
【解析】
试题分析：求出B区域圆心角在整个圆中所占的比例，这个比例即为所求的概率．
试题解析：∵B扇形区域的圆心角为120°，
所以B区域所占的面积比例为
，
即转动圆盘一次，指针停在B区域的概率是．
考点：几何概率．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
知：如图，l∥m，等边△ABC的顶点B在直线m上，边BC与直线m所夹锐角为20°，则∠α的度数为( )
有两个不相等实数根的概率．某射击运动员在相同条件下的射击160次，其成绩记录如下：
射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
射中9环以上的次数 | 15 | 33 | 63 | 79 | 97 | 111 | 130 | |
射中9环以上的频率 | 0．75 | 0．83 | 0．80 | 0．79 | 0．79 | 0．79 | 0．81 |
（1）根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0．01）；
（2）根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0．1），并简述理由．
C．
D．
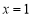，与x轴交于A、B两点，若B点坐标是
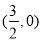，则A点的坐标是 .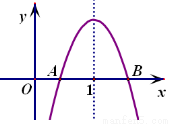 
的相反数是（ ）
D．