题目内容
如图，抛物线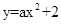
与y轴交于点A，抛物线上的一点P在第四象限，连接AP与x轴交于点C，
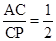，且S△AOC=1，过点P作PB⊥y轴于点B．
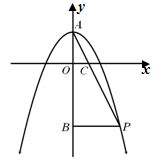
（1）求BP的长；
（2）求抛物线与x轴的交点坐标．
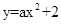与y轴交于点A，抛物线上的一点P在第四象限，连接AP与x轴交于点C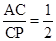，，且S△AOC=1，过点P作PB⊥y轴于点B．（1）求BP的长；
（2）求抛物线与x轴的交点坐标．
（1）3；（2）（
，0），（
，0）．
，0），（，0）．试题解析：（1）当x=0时，y=2，∴OA=2，∵
，∴OC=1，∵PB⊥y轴，∴OC∥BP，∴△AOC∽△ABP，∴
，∴BP=3；（2）由（1）得P（3，－4），将点P（3，－4）代入
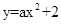得，
，∴
，∴
，当y=0时，
，∴
，
，∴抛物线与x轴的交点坐标是（，0），（，0）．
练习册系列答案
阅读快车系列答案
相关题目
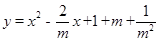顶点的纵坐标y与横坐标x之间的关系式.
>1
的图象经过点P（-3，2），则该图象必经过点（ ）
与双曲线
的交点A的横坐标是1，则关于
的不等式
的解集是（ ）
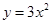先向上平移3个单位，再向左平移2个单位后得到的抛物线解析式为（ ）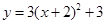
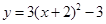
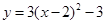
的最小值是 ．
的图象的顶点坐标是（ ）