题目内容
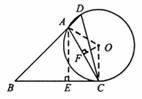
如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3 ,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
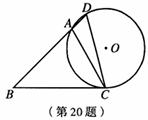
解:(1)过点A作AE⊥BC,垂足为E.
∴∠AEB=∠AEC=90°.
在Rt△ABE中,∵sinB=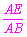 ,
,
∴AB=AB·sinB=3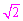 ·sin45°= 3
·sin45°= 3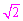 ·
·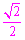 =3.
=3.
∵∠B=45°,
∴∠BAE=45°.
∴BE=AE=3.
在Rt△ACE中,∵tan∠ACB=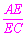 ,
,
∴EC=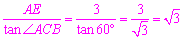 .
.
∴BC=BE+EC=3+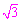 .
.

(2)由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=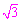 ,
,
∴AC=2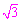 .
.
解法一:连接AO并延长交⊙O于M,连接CM.
∵AM为直径,
∴∠ACM=90°.
在Rt△ACM中,∵∠M=∠D=∠ACB=60°,sinM=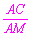 ,
,
∴AM= =
=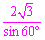 =4.
=4.
∴⊙O的半径为2.
解法二:连接OA,OC,过点O作OF⊥AC,垂足为F,
则AF=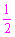 AC=
AC=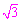 .
.
∵∠D=∠ACB=60°,
∴∠AOC=120°.
∴∠AOF=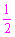 ∠AOC=60°.
∠AOC=60°.
在Rt△OAF中,sin∠AOF=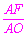 ,
,
∴AO=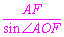 =2,即⊙O的半径为2.
=2,即⊙O的半径为2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两
种植户种植的两类蔬菜的种植面积与总收入如下表:
| 种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) | 每亩成本(单位:元)
|
| 甲 | 3 | 1 | 12500 | 1400 |
| 乙 | 2 | 3 | 16500 | 1600 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
⑴ 求A、B两类蔬菜每亩平均收入各是多少元?
⑵ 某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户的最大利润方案.
 )与点P移动的时间t(单位:s)的函数关系式如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).
)与点P移动的时间t(单位:s)的函数关系式如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).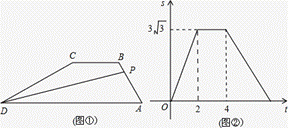
 交于E,F两点,若AB=2EF,则k的值是
交于E,F两点,若AB=2EF,则k的值是 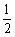 D.
D.

 .
.  D.
D. 
 的度数为
的度数为 
 几何知识解释其道理正确的是
几何知识解释其道理正确的是 不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值)
不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值)