题目内容
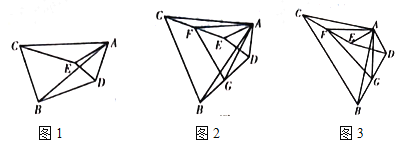
【题目】如图1,将![]() 以点A为中心,逆时针旋转
以点A为中心,逆时针旋转![]() 得到
得到![]() .
.
(1)若![]() ,求
,求![]() 的度数:
的度数:
(2)当![]() 时,如图2,点F、G分别是CE、BD的中点,证明:
时,如图2,点F、G分别是CE、BD的中点,证明:![]() 是等边三角形;
是等边三角形;
(3)当![]() 时,如图3,点F、G分别是CE、BD的中点,直接判断
时,如图3,点F、G分别是CE、BD的中点,直接判断![]() 的形状,不需要说明理由.
的形状,不需要说明理由.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)根据旋转的性质即得![]() ,
,![]() ,进一步即得
,进一步即得![]() ,然后在△ADE中根据三角形的内角和定理求解即可;
,然后在△ADE中根据三角形的内角和定理求解即可;
(2)由旋转的性质可得![]() ,于是有
,于是有![]() ,
,![]() ,
,![]() ,再根据点F、G分别是CE、BD的中点,可得
,再根据点F、G分别是CE、BD的中点,可得![]() ,然后利用SAS可推出
,然后利用SAS可推出![]() ,进而得AF=AG,∠FAE=∠GAD,进一步即得∠FAG=60°,问题即得解决;
,进而得AF=AG,∠FAE=∠GAD,进一步即得∠FAG=60°,问题即得解决;
(3)仿(2)的思路可证得:AF=AG,∠FAG=∠EAD=90°,进而可对△AFG的形状作出判断.
解:(1)由旋转的性质,可得:![]() ,
,![]() .
.
![]() ,即
,即![]() .
.
![]() .
.
(2)证明:由旋转的性质易知![]() .
.
![]() ,
,![]() ,
,![]() .
.
又![]() 点F、G分别是CE、BD的中点,
点F、G分别是CE、BD的中点,
∴![]() ,
,![]() .
.
![]() .
.
∴AF=AG,∠FAE=∠GAD,
![]()
![]()
![]() .
.
![]() 是等边三角形.
是等边三角形.
(3)证明:由旋转的性质易知![]() .
.
![]() ,
,![]() ,
,![]() .
.
又![]() 点F、G分别是CE、BD的中点,
点F、G分别是CE、BD的中点,
∴![]() ,
,![]() .
.
![]() .
.
∴AF=AG,∠FAE=∠GAD,
![]()
![]()
![]() .
.
![]() 是等腰直角三角形.
是等腰直角三角形.

练习册系列答案
相关题目