题目内容
（2013•莆田）如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角等于（ ）分析：根据直角三角形两锐角互余求出∠BAC，然后求出∠BAB′，再根据旋转的性质对应边的夹角∠BAB′即为旋转角．
解答：解：∵∠B=35°，∠C=90°，
∴∠BAC=90°-∠B=90°-35°=55°，
∵点C、A、B1在同一条直线上，
∴∠BAB′=180°-∠BAC=180°-55°=125°，
∴旋转角等于125°．
故选C．
∴∠BAC=90°-∠B=90°-35°=55°，
∵点C、A、B1在同一条直线上，
∴∠BAB′=180°-∠BAC=180°-55°=125°，
∴旋转角等于125°．
故选C．
点评：本题考查了旋转的性质，直角三角形两锐角互余的性质，熟练掌握旋转的性质，明确对应边的夹角即为旋转角是解题的关键．
练习册系列答案
华东师大版一课一练系列答案
相关题目
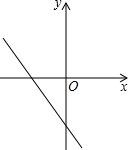（2013•莆田）如图，一次函数y=（m-2）x-1的图象经过二、三、四象限，则m的取值范围是（ ）
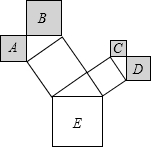（2013•莆田）如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别为2，5，1，2．则最大的正方形E的面积是
（2013•莆田）如图，抛物线y=ax2+bx+c的开口向下，与x轴交于点A（-3，0）和点B（1，0）．与y轴交于点C，顶点为D．