题目内容
 在矩形纸片ABCD中,AB=12,BC=16.
在矩形纸片ABCD中,AB=12,BC=16.(1)将矩形纸片沿BD折叠,使点A落在点E处(如图①),设DE与BC相交于点F,求BF的长;
(2)将矩形纸片如图②折叠,使点B与点D重合,折痕为GH.求GH的长.
分析:由翻折,找着重合的部分,得到相等的边,相等的角,设出未知数,用未知数表示出相关的量,应用勾股定理,列出方程可求得答案.
解答:解:过点H作HE⊥AD,垂足为E,
(1)设BF=x,则FC=16-x,
∵BD为折痕,
∴∠ADB=EDB,
又∠ADB=∠DBC,
∴∠DBC=∠BDE,
∴DF=BF=x,
Rt△DCF中,
x2=(16-x)2+122,
解得x=
;
BF=
.
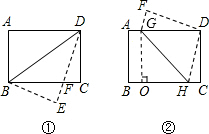
(2)过点G作GO垂直于BC,
解:(先算出HC的长度,并设为x),
因为折叠,所以DH=BH,
又因为矩形ABCD所以利用勾股定理得,
HC2+DC2=BH2,
x2+12×12=(16-x)2,
解得x=3.5,
∵∠FDG+∠ADH=90°,∠HDC+∠ADH=90°,
∴∠HDC=∠FDG,
在△DHC和△DGF中,
∵
,
∴△DHC≌△DGF(ASA),
∴FG=AG=HC=3.5,
所以OH=9,
HO2+GO2=GH2,
9×9+12×12=GH2,
GH=15.
(1)设BF=x,则FC=16-x,
∵BD为折痕,
∴∠ADB=EDB,
又∠ADB=∠DBC,
∴∠DBC=∠BDE,
∴DF=BF=x,
Rt△DCF中,
x2=(16-x)2+122,
解得x=
| 25 |
| 2 |
BF=
| 25 |
| 2 |

(2)过点G作GO垂直于BC,
解:(先算出HC的长度,并设为x),
因为折叠,所以DH=BH,
又因为矩形ABCD所以利用勾股定理得,
HC2+DC2=BH2,
x2+12×12=(16-x)2,
解得x=3.5,
∵∠FDG+∠ADH=90°,∠HDC+∠ADH=90°,
∴∠HDC=∠FDG,
在△DHC和△DGF中,
∵
|
∴△DHC≌△DGF(ASA),
∴FG=AG=HC=3.5,
所以OH=9,
HO2+GO2=GH2,
9×9+12×12=GH2,
GH=15.
点评:本题考查了翻折变换问题;找准相等的量,结合勾股定理进行解题是做这类题目的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
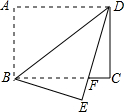 在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.
在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.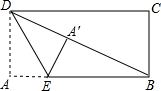 (2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为
(2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 (2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F; 如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为
如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.