题目内容
正方形ABCD的边长为6,⊙O过B、C两点,⊙O的半径为 ,连接AO,则tan∠BAO=________.
,连接AO,则tan∠BAO=________.
 或
或
分析:先根据题意画出图形,由于⊙O的圆心在正方形ABC的内部与外部不能确定,故应分两种情况讨论:
①当⊙O的圆心在正方形ABCD的外部时,连接OB,过O作OG⊥AD于点G,交BC于点F,由垂径定理可知OF是BC的垂直平分线,再根据勾股定理求出OF的长,由相似三角形的判定定理得出Rt△OEF∽Rt△OAG,再由相似三角形的对应边成比例即可求出EF的长,由锐角三角函数的定义即可得出tan∠BAO的值;
②当⊙O的圆心在正方形ABCD的外部时,连接OB,过O作OF⊥BC,OE⊥AB,E、F为垂足,由垂径定理可知OF垂直平分BC,进而可得出BF的长,由勾股定理可求出OF的长,由锐角三角函数的定义即可得出tan∠BAO的值.
解答:
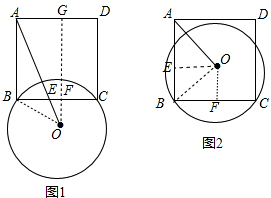 解:①当⊙O的圆心在正方形ABCD的外部时,如图1所示:
解:①当⊙O的圆心在正方形ABCD的外部时,如图1所示:连接OB,过O作OG⊥AD于点G,交BC于点F,
∵AD∥BC,OG⊥BC,
∴OF是BC的垂直平分线,
∵BC=6,
∴BF=AG=3,
∵OB=
 ,
,∴OF=
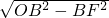 =
=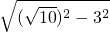 =1,
=1,在Rt△OEF与Rt△OAG中,
∵BC∥AD,
∴Rt△OEF∽Rt△OAG,
∴
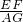 =
=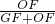 ,即
,即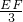 =
=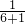 ,解得EF=
,解得EF= ,
,∵BC⊥AB,
∴tan∠BAO=
 =
=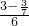 =
= ;
;②当⊙O的圆心在正方形ABCD的外部时,如图2所示:
连接OB,过O作OF⊥BC,OE⊥AB,E、F为垂足,由垂径定理可知OF垂直平分BC,
∵BC=6,
∴BF=
 BC=
BC= ×6=3,
×6=3,∵四边形OEBF的四个角均为直角,
∴OE=BF=3,OF=BE,
在Rt△OBF中,OF=
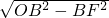 =
=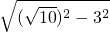 =1,
=1,∴BE=1,AE=AB-BE=6-1=5,
∴tan∠BAO=
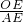 =
= .
.故答案为:
 或
或 .
.点评:本题考查的是垂径定理、正方形的性质、勾股定理及锐角三角函数的定义,解答此题时要注意分类讨论,不要漏解.

练习册系列答案
相关题目
 附加题
附加题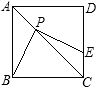 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3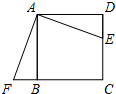 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=