题目内容
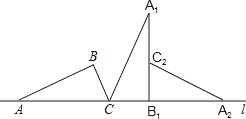
【题目】如图，把直角△ABC的斜边AC放在直线l上，按顺时针的方向在直线l上转动两次，使它转到△A2B1C2的位置，设AB＝
，∠BAC＝30°，则顶点A运动到点A2的位置时，点A所经过的路线为（ ）
A. （ 
+
）π B. （
+）π C. 2π D. π
【答案】A
【解析】
A点所经过的弧长有两段，①以C为圆心，CA长为半径，∠ACA1为圆心角的弧长；②以B1为圆心，AB长为半径，∠A1B1A2为圆心角的弧长．分别求出两段弧长，然后相加即可得到所求的结论．
在Rt△ABC中，AB＝
，∠BAC＝30°，
∴∠ACB＝60°，AC＝2；
由分析知：点A经过的路程是由两段弧长所构成的：
①A～A1段的弧长：L1＝
，
②A1～A2段的弧长：L2＝
，
∴点A所经过的路线为（
+
）π，
故选A．
练习册系列答案
相关题目
