题目内容
 如图,直线
如图,直线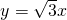 向右平移a个单位后得到直线l,l与函数
向右平移a个单位后得到直线l,l与函数 (x>0)相交于点A,与x轴相交于点B,且OB=AB,若OA2-OB2=8,则k=________.
(x>0)相交于点A,与x轴相交于点B,且OB=AB,若OA2-OB2=8,则k=________.

分析:过A作AC垂直于x轴交x轴于C,因为直线l是由y=
 x平移得到的,所以直线l与x轴的夹角∠ABC=60°,由OB=BA得到∠AOB与∠OAB相等都等于30°,且∠BAC=30°,设出AC的长,表示出OA和OB,代入已知的OA2-OB2=8中,即可求出AC和OC的长确定出点A的坐标,把求出的A的坐标代入到反比例解析式y=
x平移得到的,所以直线l与x轴的夹角∠ABC=60°,由OB=BA得到∠AOB与∠OAB相等都等于30°,且∠BAC=30°,设出AC的长,表示出OA和OB,代入已知的OA2-OB2=8中,即可求出AC和OC的长确定出点A的坐标,把求出的A的坐标代入到反比例解析式y= 中,即可求出k的值.
中,即可求出k的值.解答:
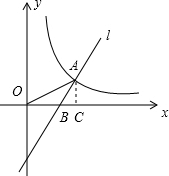 解:如图,过A作AC垂直于x轴交x轴于C,
解:如图,过A作AC垂直于x轴交x轴于C,由直线l是直线y=
 x平移得到的,所以tan∠ABC=
x平移得到的,所以tan∠ABC= ,即∠ABC=60°,
,即∠ABC=60°,又OB=AB,所以∠AOB=∠OAB=30°,
设AC=m,则OA=2m,根据勾股定理得到OC=
 m,
m,又△ABC为直角三角形,∠BAC=30°,
则tan30°=
 ,即BC=
,即BC= m,
m,所以OB=OC-BC=
 m-
m- m=
m= m,
m,又∵OA2-OB2=8,即4m2-
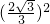 m2=8,
m2=8,解得:m=
 ,
,则OC=3,AC=
 ,即点A坐标为(3,
,即点A坐标为(3, ),
),把A坐标代入y=
 中,得到k=3
中,得到k=3 .
.故答案为:3
 .
.点评:此题考查30°角的直角三角形的性质,勾股定理以及待定系数法求反比例解析式.解本题的关键是平移前后的两直线平行,得到两直线与x轴所夹的锐角相等,求出∠ABC的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
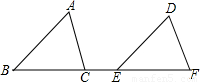
 8、如图,△ABC向右平移后得到△DEF,且点B、C、E、F在同一直线上,已知BF=8,CE=2,则平移的距离是
8、如图,△ABC向右平移后得到△DEF,且点B、C、E、F在同一直线上,已知BF=8,CE=2,则平移的距离是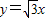 向右平移a个单位后得到直线l,l与函数
向右平移a个单位后得到直线l,l与函数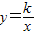 (x>0)相交于点A,与x轴相交于点B,且OB=AB,若OA2-OB2=8,则k= .
(x>0)相交于点A,与x轴相交于点B,且OB=AB,若OA2-OB2=8,则k= .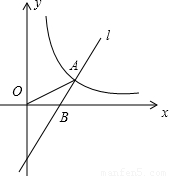
 如图,△ABC向右平移后得到△DEF,且点B、C、E、F在同一直线上,已知BF=8,CE=2,则平移的距离是________.
如图,△ABC向右平移后得到△DEF,且点B、C、E、F在同一直线上,已知BF=8,CE=2,则平移的距离是________.