题目内容
如图,在直角坐标系中,四边形OABC是矩形,OA=3,OC=4,P为直线AB上一动点,将直线OP绕点P逆时针旋转90o交直线BC于点Q。
(1)当点P在线段AB上运动(不与A,B重合)时,求证:
(2)在(1)成立的条件下,设点P的横坐标为m,线段CQ的长度为L,求出L关于m的函数解析式,并判断L是否存在最小值,若存在求出最小值,若不存在,请说明理由。
(3)在直线AB上是否存在点P,使ΔPOQ为等腰三角形,若存在,求出点P的坐标,若不存在,请说明理由。
 |
(1)证明:∵∠APO+∠AOP=900 ∠APO+∠BPQ= 900 ∴∠AOP=∠BPQ
 ∴RtΔAPO∽RtΔBQP
∴RtΔAPO∽RtΔBQP
∴
∴OA·BQ=AP·BP
(2)∵OA·BQ=AP·BP
 ∴3(3-L)=m(4-m)
∴3(3-L)=m(4-m)
∴L关于m的解析式为
∵a=1/3>0则L有最小值 L最小值=5/3
(3)存在,理由 ∵OP⊥PQ则OP=PQ
ΔAPO∽ΔBQP
∴OA/BP=PO/PQ=1 即OA=BP=3
∴AP=1
∴直线AB上存在点P,使ΔPOQ为等腰三角形,点P的坐标为(1,3)

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
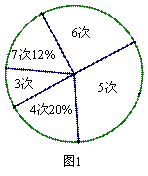
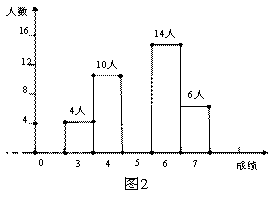 为了解某校九年级男生体育测试情况,体育老师随机抽取部分男生进行测试,并对成绩进行统计,绘制成图1和图2两幅。尚不完整的统计图
为了解某校九年级男生体育测试情况,体育老师随机抽取部分男生进行测试,并对成绩进行统计,绘制成图1和图2两幅。尚不完整的统计图
 |
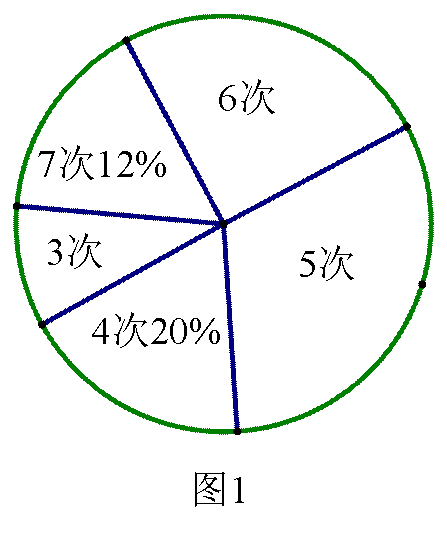
(1) 求本次抽测的男生______人。
(2) 将两幅图补充完整。
(3) 若规定引体向上5次以上(含5次)为达标,则该校350名九年级男生估计有多少人能达标?
 AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3

 、
、 在数轴上的位置如图所示,则
在数轴上的位置如图所示,则 的值是( )
的值是( )
 为圆心的圆弧与
为圆心的圆弧与 轴交于
轴交于 两点,点
两点,点 的坐标为(2,0),则点
的坐标为(2,0),则点 的坐标为 .
的坐标为 . 