��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У��ı���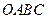 Ϊ���Σ�
����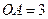 ��
��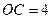 ��
�� Ϊֱ��
Ϊֱ��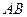 ��һ���㣬��ֱ��
��һ���㣬��ֱ��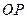 �Ƶ�
�Ƶ� ��ʱ�뷽����ת
��ʱ�뷽����ת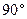 ��ֱ��
��ֱ��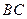 �ڵ�
�ڵ�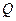 ��
��

��1������ ���߶�
���߶�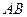 ���˶�������
���˶�������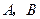 �غϣ�ʱ����֤��OA��BQ=AP��BP��
�غϣ�ʱ����֤��OA��BQ=AP��BP��
��2���ڣ�1�������������£���� �ĺ�����Ϊ
�ĺ�����Ϊ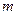 ���߶�
���߶�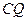 �ij���Ϊ
�ij���Ϊ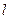 �����
�����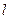 ����
����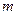 �ĺ�������ʽ�����ж�
�ĺ�������ʽ�����ж�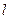 �Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɡ�
�Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɡ�
��3��ֱ��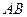 ���Ƿ���ڵ�
���Ƿ���ڵ� ��ʹ
��ʹ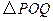 Ϊ���������Σ������ڣ��������
Ϊ���������Σ������ڣ�������� �����ꣻ�������ڣ���˵�����ɡ�
�����ꣻ�������ڣ���˵�����ɡ�
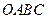 ����
����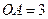 ��
��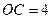 ��
�� Ϊֱ��
Ϊֱ��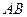 ��һ���㣬��ֱ��
��һ���㣬��ֱ��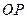 �Ƶ�
�Ƶ� ��ʱ�뷽����ת
��ʱ�뷽����ת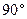 ��ֱ��
��ֱ��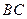 �ڵ�
�ڵ�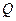 ��
��
��1������
 ���߶�
���߶�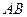 ���˶�������
���˶�������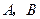 �غϣ�ʱ����֤��OA��BQ=AP��BP��
�غϣ�ʱ����֤��OA��BQ=AP��BP����2���ڣ�1�������������£����
 �ĺ�����Ϊ
�ĺ�����Ϊ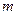 ���߶�
���߶�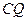 �ij���Ϊ
�ij���Ϊ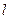 �����
�����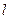 ����
����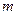 �ĺ�������ʽ�����ж�
�ĺ�������ʽ�����ж�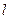 �Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɡ�
�Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɡ���3��ֱ��
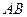 ���Ƿ���ڵ�
���Ƿ���ڵ� ��ʹ
��ʹ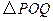 Ϊ���������Σ������ڣ��������
Ϊ���������Σ������ڣ�������� �����ꣻ�������ڣ���˵�����ɡ�
�����ꣻ�������ڣ���˵�����ɡ���
��1��֤�������ı���OABCΪ����
���OAP=��QBP=90�㣬
�ߡ�OPQ=90��, ���APO+��BPQ=90 =��APO+��AOP
=��APO+��AOP
���BPQ=��AOP, ���AOP�ס�BPQ
��
��OA��BQ=AP��BP ----------------------3��
(2) �ɣ�1��֪OA��BQ=AP��BP ��3��BQ="m(4-m) " ��BQ=
��CQ=3- =
=
��L= (0��m��4)
(0��m��4)
=
�൱m="2" ʱ�� L����С��= -----------------6��
-----------------6��
(3)�ߡ�OPQ=90��,��Ҫʹ��POQΪ���������Σ���PO="PQ" .
����P���߶�AB��ʱ����ͼ

AOP�ա�BPQ ��PB="AO=3 "
��AP=4-3=1
�� (1,3)
(1,3)
����P���߶�AB���ӳ�����ʱ����ͼ


��ʱ��QBP�ա�PAO
��PB="AO=3 " ��AP="4+3=7 "
�� (7,3)
(7,3)
����P���߶�AB�ķ����ӳ�����ʱ����ͼ

��ʱ��PB��AB��AO,
���PQB���������OPAȫ��,
��PQ��������PO���,
��ʱ��P������.
����������֪���� (1,3),
(1,3),  (7,3). ---------------9��
(7,3). ---------------9��
���OAP=��QBP=90�㣬
�ߡ�OPQ=90��, ���APO+��BPQ=90
 =��APO+��AOP
=��APO+��AOP���BPQ=��AOP, ���AOP�ס�BPQ
��

��OA��BQ=AP��BP ----------------------3��
(2) �ɣ�1��֪OA��BQ=AP��BP ��3��BQ="m(4-m) " ��BQ=

��CQ=3-
 =
=
��L=
 (0��m��4)
(0��m��4)=

�൱m="2" ʱ�� L����С��=
 -----------------6��
-----------------6��(3)�ߡ�OPQ=90��,��Ҫʹ��POQΪ���������Σ���PO="PQ" .
����P���߶�AB��ʱ����ͼ

AOP�ա�BPQ ��PB="AO=3 "
��AP=4-3=1
��
 (1,3)
(1,3)����P���߶�AB���ӳ�����ʱ����ͼ


��ʱ��QBP�ա�PAO
��PB="AO=3 " ��AP="4+3=7 "
��
 (7,3)
(7,3) ����P���߶�AB�ķ����ӳ�����ʱ����ͼ

��ʱ��PB��AB��AO,
���PQB���������OPAȫ��,
��PQ��������PO���,
��ʱ��P������.
����������֪����
 (1,3),
(1,3),  (7,3). ---------------9��
(7,3). ---------------9��
��ϰ��ϵ�д�
�����Ŀ
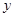 ����ȷ����P��ʹ��AOPΪ���������Σ��������������_______����
����ȷ����P��ʹ��AOPΪ���������Σ��������������_______����
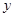 ��
��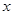 ֮��ĺ�����ϵ��ͼ����
֮��ĺ�����ϵ��ͼ����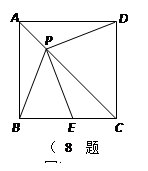
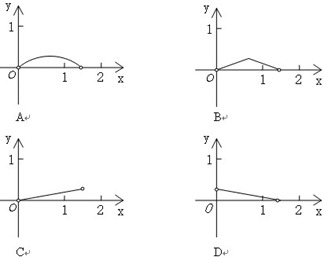

 �Ķ��㶼�ڸ���ϣ��ڷ���ֽ�н���ƽ��ֱ������ϵ��ͼ��ʾ��
�Ķ��㶼�ڸ���ϣ��ڷ���ֽ�н���ƽ��ֱ������ϵ��ͼ��ʾ��
 ��ĶԳ�ͼ�Ρ�
��ĶԳ�ͼ�Ρ� ����д����
����д���� ˳ʱ����ת
˳ʱ����ת �õ���
�õ��� ����ͼ�л�����
����ͼ�л�����