题目内容
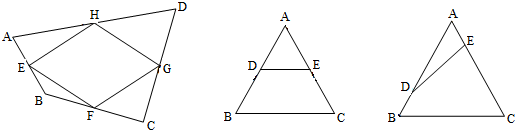
顺次连接四边形ABCD的各边中点所围成的图形是菱形，那么四边形ABCD的对角线
- A.互相平分
- B.互相垂直
- C.互相垂直平分
- D.相等
D
分析：新图形为菱形，那么各边相等，各边都等于原四边形对角线的一半，那么原四边形对角线相等即可．
解答：顺次连接四边形ABCD的各边中点所围成的图形是平行四边形，如图
DG平行且等于
AC，
EF平行且等于AC，
故HG平行且等于EF，
同理HE平行且等于GF平行且等于BD，
若EFGH为菱形，则必须HE=HG，
∴AC=BD．
故选D．
点评：本题考查菱形的判定和三角形中位线定理．主要应用了三角形中位线定理得到各边与原四边形对角线的关系．
分析：新图形为菱形，那么各边相等，各边都等于原四边形对角线的一半，那么原四边形对角线相等即可．
解答：顺次连接四边形ABCD的各边中点所围成的图形是平行四边形，如图
DG平行且等于
AC，EF平行且等于
AC，故HG平行且等于EF，
同理HE平行且等于GF平行且等于
BD，若EFGH为菱形，则必须HE=HG，
∴AC=BD．
故选D．
点评：本题考查菱形的判定和三角形中位线定理．主要应用了三角形中位线定理得到各边与原四边形对角线的关系．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=
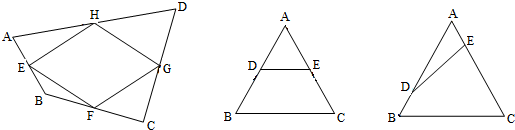
如图，在边长为1的正方形网格中，△A′B′C′与△ABC是中心对称图形．
