题目内容
已知AB=AC,DB=DE,∠BAC=∠BDE=α.
(1)若α=60°(如图1)探究线段AD与CE的数量关系,并加以证明;
(2)若α=120°,并且点D在线段AB上,(如图2)则线段AD与CE的数量关系为______;(直接写出答案)
(3)探究线段AD与CE的数量关系(如图3)并加以证明.

 解:(1)AD=CE.
解:(1)AD=CE.证明:连接BC、BE,
∵AB=AC∠BAC=60°,
∴△ABC是等边三角形.
同理△DBE也是等边三角形.
∴AB=BCBD=BE∠ABC=∠DBE=60°.
∴∠ABD=∠ABC-∠DBC=∠DBE-∠DBC=∠CBE.
∴△ABD≌△CBE.
∴AD=CE.
(2)∵∠DEB=30°=∠ACB,

∴B,E,C三点共线.
∵DE∥AC,
∴CE:AD=BE:BD.
过D作DF⊥BE于F,则BE=2BF,
∵BF:BD=cos∠B=cos30°,
∴CE:AD=2cos30°.
∴AD=
 CE.
CE.(3)连接BC、BE,

∵AB=AC,DB=DE,∠BAC=∠BDE,
∴△ABC∽△DBE.
∴
 ,∠ABC=∠DBE.
,∠ABC=∠DBE.∴
 .
.∠ABD=∠ABC-∠DBC=∠DBE-∠DBC=∠CBE,
∴△ABD∽△CBE,
∴
 .
.作DH⊥BE于H,
∵DB=DE,
∴∠BDH=
 ∠BDE=
∠BDE= ,
,BE=2BH=2BD•sin∠BDH=2BD•sin
 .
.∴
 .
.即CE=2•AD•sin
 .
.分析:(1)要探究线段AD与CE的数量关系,观察图形,猜测它们相等.而AD,CE不在同一个三角形中,因此要使AD,CE所在的三角形全等.为此连接BC、BE,证明△ABD≌△CBE,得出结论.
(2)过D作DF⊥BE于F,则BE=2BF,根据已知及三角函数即可得到结论.
(3)要探究线段AD与CE的数量关系,需使AD,CE成为相似三角形的对应边,为此连接BC、BE,证明△ABD∽△CBE,得出AD:CE=BD:BE,在等腰△BDE中根据三角函数的定义用顶角的代数式表示BD:BE,求出结果.
点评:本题综合考查了全等三角形及相似三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
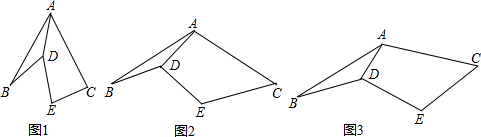
 25、如图,已知AB=AC,DB=DC,P是AD上一点,求证:∠ABP=∠ACP.
25、如图,已知AB=AC,DB=DC,P是AD上一点,求证:∠ABP=∠ACP.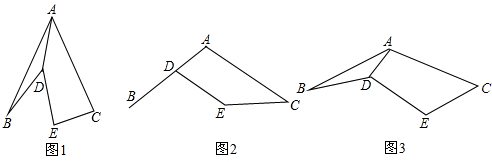
 如图,已知AB=AC,DB=DC,试说明∠ABD=∠ACD.
如图,已知AB=AC,DB=DC,试说明∠ABD=∠ACD.