题目内容
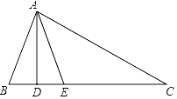
【题目】如图所示，在
中，
于
，
平分
，
，
，求
和
的度数.对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）.
解：∵，平分（______）
∴
______
______
______.（角平分线的定义）
∵（已知）
∴
______
____________.（______）
∵
（______）
∴
（等式的性质）
______（等量代换）
______.
∵于（已知）
∴
（______）
在直角三角形
中，
∵
（______）
∴
（等式的性质）
______（等量代换）
______.
【答案】见解析.
【解析】
根据条件和解题的过程步骤，对每一步的说理的依据进行明确，由什么条件得出什么结论，依据的定理、定义、法则、性质是什么，逐步进行填写和解答．
∵
，
平分
（ 已知 ）
∴
.（角平分线的定义）
∵
（已知）
∴
.（ 三角形的一个外角等于和它不相邻的两个内角的和 ）
∵
（ 平角的定义（或邻补角的定义） ）
∴
（等式的性质）
（等量代换）
.
∵
于
（已知）
∴
（ 垂直的定义 ）
在直角三角形
中
∵
（ 直角三角形的两个锐角互余 ）
∴
（等式的性质）
（等量代换）
.
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
