Question

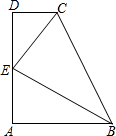在梯形ABCD中，AB∥CD，∠A=90°，AB=2，BC=3，CD=1，E是AD中点．
求证：CE⊥BE．

Answer 1

证明：延长CE交BA的延长线于点G，即交点为G，
∵E是AD中点，
∴AE=ED，
∵AB∥CD，
∴∠CDE=∠GAE，∠DCE=∠AGE，
∴△CED≌△GEA，
∴CE=GE，AG=DC，
∴GB=BC=3，
∴EB⊥EC．
分析：延长CE交BA的延长线于点G，那么可得△CED≌△GEA，那么CE=GE，AE=DE，进而可得BC=BG，那么CE⊥BE．
点评：考查梯形的常用辅助线方法的应用；碰到中点问题时构造全等三角形是常用的辅助线方法．