题目内容
已知二次函数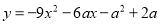 ,当
,当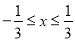 ,
, 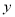 有最大值为
有最大值为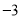 ,则
,则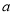 的值为_____________________.
的值为_____________________.
 阅读快车系列答案
阅读快车系列答案若分式方程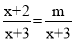 无解,则m的值为( )
无解,则m的值为( )
A. ﹣1 B. 0 C. 1 D. 3
A 【解析】去分母得:x+2=m, 由分式方程无解得到x=?3, 代入整式方程得:m=?1, 故选:A已知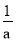 ﹣
﹣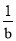 =
=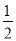 ,则
,则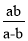 的值为( )
的值为( )
A. 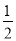 B.
B. 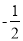 C. ﹣2 D. 2
C. ﹣2 D. 2
如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )
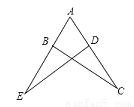
A. ∠E=∠C B. AC=AE C. ∠ADE=∠ABC D. DE=BC
查看答案如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪开后拼成一个长方形,上述操作能验证的等式是( )
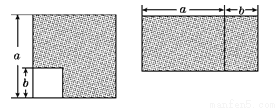
A. (a+b)(a-b)=a2-b2 B. (a-b)2=a2-2ab+b2
C. (a+b)2=a2+2ab+b2 D. a2+ab=a(a+b)
查看答案如果分式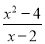 的值等于0,那么( )
的值等于0,那么( )
A. 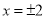 B.
B. 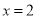 C.
C. 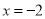 D.
D. 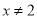
计算(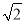 ﹣
﹣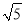 )(
)(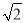 +
+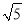 )的结果是( )
)的结果是( )
A. ﹣3 B. 3 C. 7 D. 4
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解方程:x+5=x2-25.
x1=-5,x2=6 【解析】试题分析:移项,运用因式分解法即可求出方程的解. 试题解析:x+5=x2-25 x2-x-30=0 (x+5)(x-6)=0 x+5=0,x-6=0 x1=-5,x2=6.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=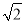 AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.
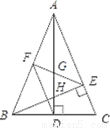
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=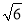 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.
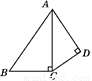
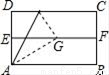
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______
设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
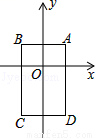
查看答案如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


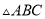 中,
中, 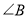 与
与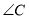 的平分线的交点
的平分线的交点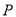 恰好在
恰好在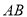 边的高
边的高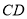 上,那么
上,那么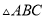 一定是( ).
一定是( ).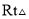 B. 等边
B. 等边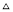 C. 等腰
C. 等腰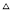 D. 等腰直角
D. 等腰直角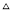
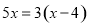 (2)
(2)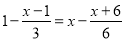
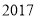 年双十一当天,天猫总成交额达
年双十一当天,天猫总成交额达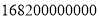 元.数
元.数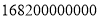 用科学记数法可表示为( )
用科学记数法可表示为( )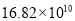 B.
B. 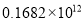 C.
C. 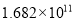 D.
D. 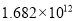
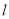 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥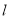 于点D.
于点D. 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小; 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.