题目内容
如图,在 ABC中,点D在边AC上,DB=BC, 点E是CD的中点,点F是AB的中点.(1) 试说明:EF=
ABC中,点D在边AC上,DB=BC, 点E是CD的中点,点F是AB的中点.(1) 试说明:EF= AB;
AB;
(2) 过点A作AG∥EF,交BE的延长线于点G,求证: ABE≌
ABE≌ AGE.
AGE.

证明:(1) 连结BE,
∵DB=BC,点E是CD的中点,∴BE⊥CD.
∵点F是Rt△ABE中斜边上的中点,∴EF= ;
;
(2) [方法一]在△ 中,
中, ,
, ,∴
,∴ .
.
在△ 和△
和△ 中,
中, ,∠AEB=∠AEG=90°,∴△ABE≌△AGE;
,∠AEB=∠AEG=90°,∴△ABE≌△AGE;
[方法二]由(1)得,EF=AF,∴∠AEF=∠FAE.
∵EF//AG,∴∠AEF=∠EAG.
∴∠EAF=∠EAG.
∵AE=AE,∠AEB=∠AEG=90°,∴△ABE≌△AGE.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 ,则第7个数是
,则第7个数是 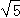 .
. ,△DEF的面积是定值.
,△DEF的面积是定值.

 B.
B. C.
C. D.
D.
 ,长度为2的线段AB在y轴上移动,设点A的坐标为(0,a).
,长度为2的线段AB在y轴上移动,设点A的坐标为(0,a).