题目内容
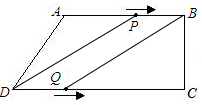
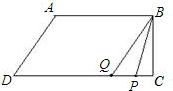
如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.

(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.

(1)16;(2) ;(3)
;(3)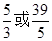 .
.
 ;(3)
;(3)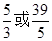 .
.试题分析:(1)过点A作AM⊥CD于M,根据勾股定理,可以求出DM=6所以DC=16.
(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图示,由题可得:BP=10-3t,DQ=2t,所以可以列出方程10-3t=2t,解得t=2,此时,BP=DQ=4,CQ=12,在△CBQ中,根据勾股定理,求出BQ即可.
(3)此题要分三种情况进行讨论:即①当点P在线段AB上,②当点P在线段BC上,③当点P在线段CD上,根据三种情况点的位置,可以确定t的值.
(1)如图,过点A作AM⊥CD于M,
根据勾股定理,AD=10,AM=BC=8,
∴
 .∴CD=16.
.∴CD=16.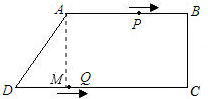
(2)当四边形PBQD为平行四边形时,
点P在AB上,点Q在DC上,如图,
由题知:BP=10-3t,DQ=2t,∴10-3t=2t,解得t=2.
此时,BP=DQ=4,CQ=12,∴
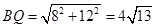 .
.∴四边形PBQD的周长=2(BP+BQ)=
 .
.
(3)①当点P在线段AB上时,即
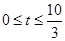 时,如图,
时,如图, ,解得
,解得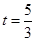 .
.
②当点P在线段BC上时,即
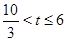 时,如图,BP=3t-10,CQ=16-2t,
时,如图,BP=3t-10,CQ=16-2t,∴
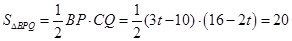 ,化简得:3t2-34t+100=0,△=-44<0,
,化简得:3t2-34t+100=0,△=-44<0,∴方程无实数解.

③当点P在线段CD上时,
若点P在Q的右侧,即
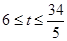 ,则有PQ=34-5t,
,则有PQ=34-5t, ,解得
,解得 <6,舍去.
<6,舍去.若点P在Q的左侧,即
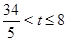 ,则有PQ=5t-34,
,则有PQ=5t-34, ,解得
,解得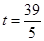 .
.综上所述,满足条件的t存在,其值分别为
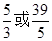 .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目


 的解是a,求关于y的方程
的解是a,求关于y的方程 的解.
的解.



 的根为 .
的根为 . 配方,化为
配方,化为 的形式应为( )
的形式应为( )


