题目内容
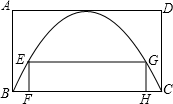
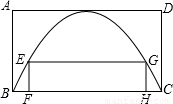
在一块矩形板ABCD上进行装饰,己知AB=2.5m,BC=4m,先在矩形板上作一抛物线,使抛物线经过B、C两点,且其顶点在AD上,再在抛物线内作另一矩形EFHG,使这矩形的一边FH在BC上,另两点E、G在抛物线上,装饰抛物线内矩形EFHG边框时,打算使用一种单价为每米30元的嵌条,由于此矩形尺寸没定,为了满足各种设计情况的需要,在作材料预算时(不计损耗),这种嵌条的预算金额至少应为多少?请建立适当的直角坐标系解决问题.

解:以BC所在的直线为x轴,抛物线的对称轴我y轴,建立平面直角坐标系,依题意设抛物线解析式:
y=ax2+2.5,
把c(2,0)代入得,a=- ,
,
∴y=- x2+2.5;
x2+2.5;
设FH=2m,则H(m,0),G(m,- m2+2.5)
m2+2.5)
即HG=- m2+2.5;
m2+2.5;
矩形EFHG的周长为:4m+2(- m2+2.5)=-
m2+2.5)=- (m-
(m- )2+
)2+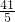 ,
,
由函数图象知
∴当m= 时,周长最大,
时,周长最大,
∴这种金额的预算金额至少为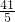 ×30=246元.
×30=246元.
分析:本题涉及抛物线与矩形的问题,应根据抛物线的位置,适当建立坐标系,求抛物线的解析式,可设小矩形中点H的坐标,从而,表达小矩形的周长,运用二次函数性质求最小值.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
y=ax2+2.5,
把c(2,0)代入得,a=-
 ,
,∴y=-
 x2+2.5;
x2+2.5;设FH=2m,则H(m,0),G(m,-
 m2+2.5)
m2+2.5)即HG=-
 m2+2.5;
m2+2.5;矩形EFHG的周长为:4m+2(-
 m2+2.5)=-
m2+2.5)=- (m-
(m- )2+
)2+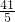 ,
,由函数图象知
∴当m=
 时,周长最大,
时,周长最大,∴这种金额的预算金额至少为
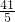 ×30=246元.
×30=246元.分析:本题涉及抛物线与矩形的问题,应根据抛物线的位置,适当建立坐标系,求抛物线的解析式,可设小矩形中点H的坐标,从而,表达小矩形的周长,运用二次函数性质求最小值.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目