题目内容
 如图,在△ABC,DE∥BC,若AD=2,BD=3,则
如图,在△ABC,DE∥BC,若AD=2,BD=3,则| DE |
| BC |
分析:由AD=3,DB=2,即可求得AB的长,又由DE∥BC,根据平行线分线段成比例定理,可得DE:BC=AD:AB,则可求得答案.
解答:解:∵AD=2,DB=3,
∴AB=AD+BD=3+2=5,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AD:AB=2:5.
故选C.
∴AB=AD+BD=3+2=5,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AD:AB=2:5.
故选C.
点评:此题考查了相似三角形的判定和性质.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
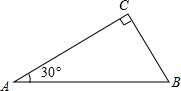 的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.
的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.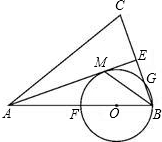 F,FB恰为⊙O的直径.
F,FB恰为⊙O的直径. 7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=
7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=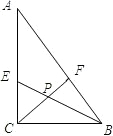 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为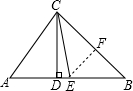 如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为
如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为