题目内容
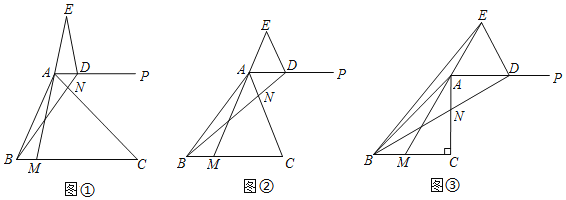
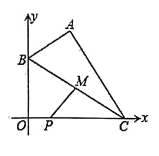
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以
出发,以![]() 的速度分别沿
的速度分别沿![]() 、
、![]() 匀速运动,当点
匀速运动,当点![]() 到达点
到达点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() .过点
.过点![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
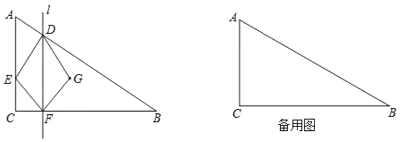
(1)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 的平分线上;
的平分线上;
(2)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 边上;
边上;
(3)设![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写
之间的函数关系式,并写![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
【解析】
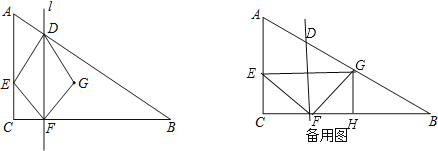
(1)过点![]() 做
做![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,所以
出发,所以![]() ,且
,且![]() 也是
也是![]() 的角平分线,由
的角平分线,由![]() 得:
得:![]() ,
,![]()
![]() ,
,![]() ,可求得
,可求得![]() 、
、![]() 的长度,由
的长度,由![]() ,
,![]() ,构造关于
,构造关于![]() 的方程可以求得答案.
的方程可以求得答案.
(2)点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由(1)中的数值,结合
,由(1)中的数值,结合![]() ,构造出关于
,构造出关于![]() 的方程,可以得到答案.
的方程,可以得到答案.
(3)由![]() 得到
得到![]() ,
,![]()
![]() ,即
,即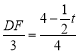 ,得到
,得到![]() ,分两种情况讨论:
,分两种情况讨论:
①当![]() 时,
时,![]() ;
;
②当![]() 时,设
时,设![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,求得
,求得![]() ,解出
,解出![]() 与
与![]() 的关系,继而求得
的关系,继而求得![]() 与
与![]() 的关系.
的关系.
解:(1)![]()
设![]() ,
,![]() 相交于
相交于![]() ,过点
,过点![]() 做
做![]() ,垂足为
,垂足为![]() ,
,![]() ,
,
垂足为![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,所以四边形
出发,所以四边形![]() 、四边形
、四边形![]() 都是正方形,
都是正方形,
![]() ,
,
又![]() 也是
也是![]() 的角平分线,
的角平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,又
,又![]() ,
,
![]()
![]() ,解得:
,解得:![]() .
.

(2)![]()
点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
![]() ,
,
所以![]() ,
,
![]()
![]() ,
,
即: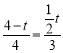 ,
,
解得:![]() .
.
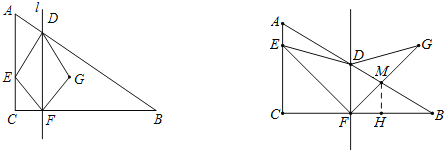
(3)![]() ,
,
![]() ,
,
![]()
![]() ,
,
即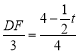 ,
,
解得![]()
①当![]() 时,
时,![]() .
.
②当![]() 时,设
时,设![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,
,
则![]() ,
,
![]()
![]() ,
,
解得![]() ,
,
![]() .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目