题目内容
已知：如图，AC⊥AB，BD⊥CD，AC与BD相交于点E，S△AED=25，S△BEC=36．求：cos∠AEB．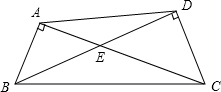
分析：首先由∠BAC=∠BDC=90°与∠AEB=∠DEC，证得△ABE∽△DCE；即可证得：
=
，又由∠AED=∠BEC，证得△AED∽△BEC，根据相似三角形面积的比等于相似比的平方，即可求得AE与BE的比值，则问题得解．
| AE |
| BE |
| DE |
| EC |
解答：解：∵AC⊥AB，BD⊥CD，
∴∠BAC=∠BDC=90°，
又∵∠AEB=∠DEC，
∴△ABE∽△DCE，
∴
=
，即
=
，
又∵∠AED=∠BEC，
∴△AED∽△BEC，
∴
=
=
，
∴在Rt△ABE中，cos∠AEB=
=
．
∴∠BAC=∠BDC=90°，
又∵∠AEB=∠DEC，
∴△ABE∽△DCE，
∴
| AE |
| DE |
| BE |
| EC |
| AE |
| BE |
| DE |
| EC |
又∵∠AED=∠BEC，
∴△AED∽△BEC，
∴
| AE |
| BE |
|
| 5 |
| 6 |
∴在Rt△ABE中，cos∠AEB=
| AE |
| BE |
| 5 |
| 6 |
点评：此题考查了相似三角形的判定与性质和三角函数的性质．此题比较简单，解题时要注意图形间的联系，掌握数形结合思想的应用．
练习册系列答案
相关题目
29、已知：如图，AC=BD，DF=CE，∠ECB=∠FDA．求证：AF=BE．
16、已知：如图，AC=DF，AC∥FD，AE=DB，则根据
是切点，
12、已知：如图，AC、BD交于O点，OA=OC，OB=OD、则不正确的结果是（ ）
已知：如图，AC平分∠BAD，CE⊥AB于E点，CF⊥AD于F点，在AB上有一点M，且CM=CD．