题目内容
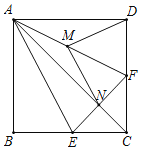
【题目】如图，在平行四边形ABCD中，点E.F分别在AB、CD上，AE=CF，连接AF，BF，DE，CE，分别交于H、G.
求证：(1)四边形AECF是平行四边形。(2)EF与GH互相平分。
【答案】见解析
【解析】
(1)根据四边形ABCD是平行四边形,由平行四边形的性质可得:
,
,
根据
,利用平行四边形的判定定理可得:四边形AECF是平行四边形,
由
得四边形AECF是平行四边形,根据平行四边形的性质可得:
,
根据,,,可得:
,
,根据平行四边形的判定定理可得:四边形BFDE是平行四边形,再根据平行四边形的性质可得:
,根据平行四边形的判定定理可得:四边形EGFH是平行四边形,由平行四边形的性质可得:
与GH互相平分.
四边形ABCD是平行四边形,
,,
,
四边形AECF是平行四边形,
由得:四边形AECF是平行四边形,
,
,,,
,,
四边形BFDE是平行四边形,
,
四边形EGFH是平行四边形,
与GH互相平分.
练习册系列答案
计算高手系列答案
相关题目
