题目内容
圆的内接矩形的周长与圆周长之比的最大值是________.
分析:先根据题意画出图形,设圆的半径为R,可表示出矩形的周长和圆的周长,根据圆内接四边形的性质即可解题.
解答:
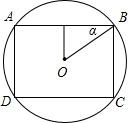 解:设圆的半径为R,如图所示:
解:设圆的半径为R,如图所示:圆的内接矩形的长AB=2Rcosα,宽BC=2Rsinα,
∴矩形周长为4R(cosα+sinα),
又圆周长为2πR,
∴周长为与圆周长之比为:
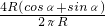 =
=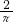 (cosα+sinα),
(cosα+sinα),=
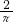 •
•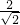 sin(45°+α)≤
sin(45°+α)≤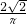 .
.故答案为:
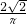 .
.点评:本题考查了圆内接四边形的性质,难度适中,关键是根据题意画出图形,题图结合,用可消去的参数表示出矩形的周长和圆的周长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
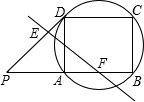 线EF能否将四边形PBCD的周长和面积同时平分?若能,请求出BF的长.若不能,请说明理由.
线EF能否将四边形PBCD的周长和面积同时平分?若能,请求出BF的长.若不能,请说明理由.