Question

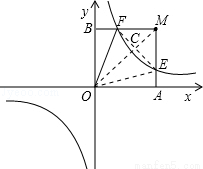
已知双曲线y=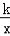（k＞0），过点M（m，m）（m＞）作MA⊥x轴，MB⊥y轴，垂足分别是A和B，MA、MB分别交双曲线y=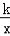（k＞0）于点E、F。

（1）若k=2，m=3，求直线EF的解析式；

（2）O为坐标原点，连接OF，若∠BOF=22.5°，多边形BOAEF的面积是2，求k值。

 

Answer 1

（1）直线EF解析式为y=﹣x+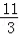 ；（2）k=1 。

【解析】

试题分析：（1）将k的值代入确定出反比例解析式，将m的值代入确定出M坐标，根据图形得到E的横坐标与F的纵坐标都为3，代入反比例解析式中确定出E与F坐标，设直线EF解析式为y=kx+b，将E与F坐标代入求出k与b的值，即可确定出直线EF的解析式；

（2）连接EF，OM，OE，由M横纵坐标相等得到四边形AOBM为正方形，由正方形的性质及∠BOF=22.5°，得到三角形BOF、三角形FCO、三角形ECO及三角形AOE全等，三角形BOF的面积等于|k|的一半，表示出四个面积之和，即为五边形BOAEF的面积，根据五边形的面积为2列出关于k的方程，求出方程的解即可得到k的值。

试题解析：（1）将k=2，m=3代入得：反比例解析式为y=，M（3，3），

∵MA⊥x轴，MB⊥y轴，

∴E的横坐标为3，F纵坐标为3，

代入反比例解析式得：E（3，），F（，3），

设直线EF解析式为y=kx+b，

将E与F坐标代入得：，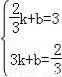

解得：，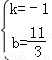

则直线EF解析式为y=﹣x+；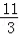

（2）连接OM，EF，OE，OM与EF交于点C，

∵M（m，m），反比例解析式为y=，

∴E（m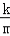，），F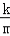（，m），即E与F关于y=x对称，四边形AOBM为正方形，

∵∠BOF=22.5°，

∴∠BOF=∠COF=∠EOC=∠AOE=22.5°，

由对称性得到∠FCO=∠ECO=90°，

在△BOF和△AOE中，

，

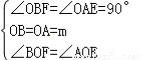∴△BOF≌△AOE（ASA），

同理△BOF≌△COF，△COF≌△AOE，

∴BF=AE=，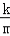

又BM=AM=m，

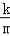∴S△BOF=m•=k，

∴S五边形BOAEF=4S△BOF=2k=2，

则k=1。

考点：反比例函数综合题。