题目内容
如图，AC，BC是两个半圆的直径，∠ACP=30°，若AB=10cm，则PQ的值（ ）
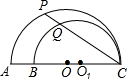
| A．5cm | B．5
| C．6cm | D．8cm |
连接AP、BQ．
∵AC，BC是两个半圆的直径，∠ACP=30°，
∴∠APQ=∠BQC=90°．
设BC=x，在Rt△BCQ中，cos∠ACP=cos30°=
=
=
，
∴QC=
x．
在Rt△APC中，cos∠ACP=cos30°=
=
=
，
解得PQ=5
cm．
故选B．
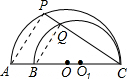
∵AC，BC是两个半圆的直径，∠ACP=30°，
∴∠APQ=∠BQC=90°．
设BC=x，在Rt△BCQ中，cos∠ACP=cos30°=
| QC |
| BC |
| QC |
| x |
| ||
| 2 |
∴QC=
| ||
| 2 |
在Rt△APC中，cos∠ACP=cos30°=
| PQ+QC |
| AB+BC |
PQ+
| ||||
| 10+x |
| ||
| 2 |
解得PQ=5
| 3 |
故选B．
练习册系列答案
相关题目
