题目内容
若m无平方根，且|m+1|=2，则m=________．
-3
分析：根据绝对值的性质求出m的值，再根据m无平方根可得m＜0，然后即可得解．
解答：∵|m+1|=2，
∴m+1=2，或m+1=-2，
解得m=1或m=-3，
∵m无平方根，
∴m＜0，
∴m=-3．
故答案为：-3．
点评：本题考查了绝对值的性质与平方根的定义，注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
分析：根据绝对值的性质求出m的值，再根据m无平方根可得m＜0，然后即可得解．
解答：∵|m+1|=2，
∴m+1=2，或m+1=-2，
解得m=1或m=-3，
∵m无平方根，
∴m＜0，
∴m=-3．
故答案为：-3．
点评：本题考查了绝对值的性质与平方根的定义，注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
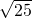的平方根是±5．