题目内容
如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2．则BD的长为（ ）
A．
B．
C．
D．
【答案】分析：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．在△BDF中，由勾股定理即可求出BD的长．
解答：
解：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．
∵DC∥AB，
∴
=
，
∴DF=CB=1，BF=2+2=4，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
=
．
故选B．
点评：本题考查了勾股定理，解题的关键是作出以A为圆心，AB长为半径的圆，构建直角三角形，从而求解．
解答：
解：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．∵DC∥AB，
∴
=，∴DF=CB=1，BF=2+2=4，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
=．故选B．
点评：本题考查了勾股定理，解题的关键是作出以A为圆心，AB长为半径的圆，构建直角三角形，从而求解．
练习册系列答案
阅读快车系列答案
相关题目
21、如图所示，四边形ABCD是平行四边形，E，F分别在AD，CB的延长线上，且DE=BF，连接FE分别交AB，CD于点H，G．
12、如图所示，四边形ABCD为⊙O的内接四边形，E为AB延长线的上一点，∠CBE=40°，则∠AOC等于（ ）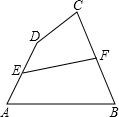
如图所示，四边形ABCD中，E、F分别为AD、BC的中点．
