Question

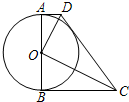如图，四边形ABCD中，AD∥BC，∠ABC=∠BAD=90°，AB为⊙O的直径．
（1）若AD=2，AB=BC=8，连接OC、OD．
①求△COD的面积；
②试判断直线CD与⊙O的位置关系，说明理由．
（2）若直线CD与⊙O相切于F，AD=x（x＞0），AB=8．试用x表示四边形ABCD的面积S，并探索S是否存在最小值，写出探索过程．

Answer 1

分析：（1）①根据S_△COD=S_梯形ABCD-S_△AOD-S_△BOC来解答；
②求直线CD与⊙O的圆心间的距离，然后根据此距离判断直线CD与⊙O的位置关系；
（2）根据勾股定理求得关于x的方程，然后求二次函数的最值即可．

解答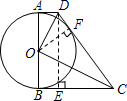：解：（1）①S_△COD=S_梯形ABCD-S_△AOD-S_△BOC
=

1

2

(AD+BC)•AB-

1

2

AD•AO-

1

2

BC•BO
=

1

2

(2+8)×8-

1

2

•2×4-

1

2

•8×4=40-4-16=20．
（或先证明△COD是直角三角形进而求其面积．）
②过D作DE⊥BC，E是垂足，从而四边形ABED是矩形．
BE=AD=2，CE=6，DE=AB=8．
在Rt△CDE中，CD=10．过O作OF⊥CD于F，
由S_△COD=

1

2

OF•CD=20，可得OF=4，
表明点O到CD的距离等于⊙O的半径，故直线CD与⊙O相切；

（2）在四边形ABCD中，
∵AD=x＞0，设BC=y，则CD=x+y，CE=|y-x|，
∴在Rt△CDE中，根据勾股定理，得
（y-x）²+64=（x+y）²，于是y=

16

x

，x＞0．
进而S=

1

2

(AD+BC)•AB=

1

2

(x+

16

x

)×8=4(x+

16

x

)，x＞0．
∵x＞0，x+

16

x

=(

x

)2-2

x

•

4

x

+(

4

x

)2+8=(

x

-

4

x

)2+8，
∴当

x

-

4

x

=0，x=4时，x+

16

x

有最小值8，从而S有最小值32．

点评：本题主要考查的是二次函数的最值、直线与圆的位置关系．