Question

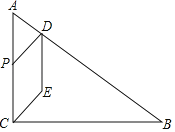
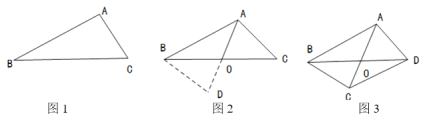
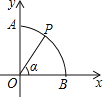
【题目】（1）某学校“学习落实”数学兴趣小组遇到这样一个题目：如图1，在中，点在线段上，，，，，求的长．经过数学小组成员讨论发现，过点作，交的延长线于点，通过构造就可以解决问题（如图2）请回答：，．

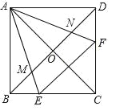
（2）请参考以上解决思路，解决问题：如图在四边形中对角线与相交于点，，，，．求的长．

Answer 1

【答案】（1），；（2）

【解析】

(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值，进而可得出AD的值，由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出;
(2)过点B作BE∥AD交AC于点E，同(1)可得出AE，在Rt△AEB中，利用勾股定理可求出BE的长度，再在Rt△CAD中，利用勾股定理可求出DC的长，此题得解．

解: (1) ，

.

又

，

.

，

故答案为：；.

(2)过点作交于点，如图所示.

，

.

,

在中，，即，解得：

在中，

.