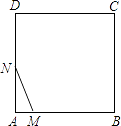题目内容
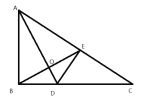
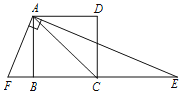
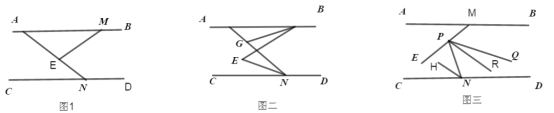
【题目】(1)如图1,![]() ,
,![]() 分别在
分别在![]() 上,试说明∠MEN=∠INC+∠IME.
上,试说明∠MEN=∠INC+∠IME.
(2)如图2,在(1)的条件下,若![]() 平分
平分![]() ,在
,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,使
,使![]() 恰好平分
恰好平分![]() ,
,![]() ,且
,且![]() 的补角比
的补角比![]() 的3倍多
的3倍多![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在问题(1)(2)的条件下,若点![]() 是
是![]() 上一动点(不包含点
上一动点(不包含点![]() 和点
和点![]() ),连接
),连接![]() .
.![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,过
,过![]() 作
作![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,下列结论:①
上运动时,下列结论:①![]() 的值不变;②
的值不变;②![]() 的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
【答案】(1)见解析;(2)40°;(3)②正确,证明见解析
【解析】
(1)在△IEM中,利用外角∠MEN=∠NIM+∠IME推导得到;
(2)先求出∠CNF的值,进而得到∠NFM,然后利用∠FNC与∠MGN的关系得到∠MGN的大小,最后在△FGM中得出∠FMG的大小,进而得出∠FME;
(3)求出∠RPQ=∠4-∠NPR=∠4―∠1,然后在△PKN中,利用内角和180°可算出∠RPQ为定值.
(1)∵AB∥CD
∴∠MIN=∠INC
∵∠MEN=∠MIN+∠IME
∴∠MEN=∠INC+∠IME;
(2)∵∠ENC=19°,EN平分∠FNC
∴∠FNC=38°=∠MFN
∵![]() 的补角比
的补角比![]() 的3倍多
的3倍多![]()
∴180°-∠MGN=3×38°+8°
∴∠MGN=58°
∴AMG=∠MGN-∠MFN=20°
∴∠AME=40°;
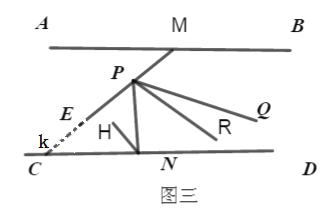
(3)如下图,延长ME交CD于点K,设∠HNP为∠1,∠HNK为∠2,∠MPQ为∠3,∠QPN为∠4
∵AB∥CD
∴∠AME=∠MKN=40°
∵PQ平分∠MPN,NH平分∠PNC
∴∠1=∠2,∠3=∠4
∵PR∥NH
∴∠1=∠NPR
∴∠RPQ=∠4-∠NPR=∠4―∠1
在△PKN中,∠1+∠2+180°-∠3-∠4+40°=180°
∴2(∠4-∠1)=40°
∴∠4-∠1=20°
∴∠RPQ=20°不变,②正确

【题目】在学校组积的科学家素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为90分、80分、70 分、60 分,学校将八年级(1)班和(2) 班的成绩整理并绘制成如下的统计图:
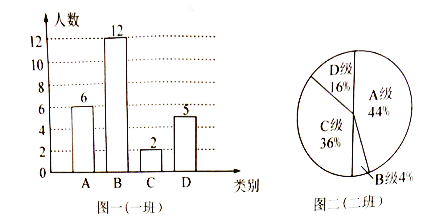
请你根据以上提供的信息解答下列问题:
(1) 此次竞赛中二 班成绩在70分以上(包括70分) 的人数有多少人?
(2) 补全下表中空缺的三个统计量:
平均数/ 分 | 中位数/ 分 | 众数/ 分 | |
一班 | 77.6 | 80 | _____________ |
二班 | _____________ | ______________ | 90 |
(3) 请根据上述图表对这次竞赛成绩进行分析,写出两个结论.