题目内容
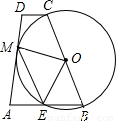
已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M。
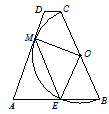
(1)求证:△EOM为等腰直角三角形;
(2)求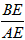 的值。
的值。
(2)求
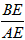 的值。
的值。| 解:(1)证明:∵OM=OE ∴∠1=∠2=67.5°, ∵等腰梯形ABCD, ∴∠1=∠2=67.5°, ∴∠1=∠A, ∴OE∥AD, ∵AD与⊙O相切于M, ∴OM⊥AD, ∴OE⊥OM, ∴△EOM为等腰直角三角形; (2)设⊙O的半径为r,OE=OM=r, 由(1)可知,∴∠OEM=45°, ∴ME=  r, r,∵∠3=180°-(∠OME+∠1)=180°-(67.5°+45°)=67.5°, ∴△AME∽△EOB, ∴BE∶AE=OE∶ME, ∴BE∶AE=r∶  r=1∶ r=1∶ = = ∶2。 ∶2。 |
 |

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
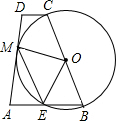 已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;
已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;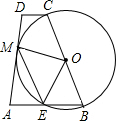 已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;
已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;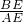 的值.
的值.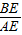 的值.
的值.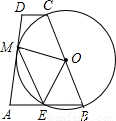
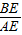 的值.
的值.