Question

如图，一根粗细均匀、长为2米的钢管AB，靠在一面与水平地面垂直的墙上，此时钢管与水平面所成的锐角为75°；当A点向下滑动到A′点时，测得钢管与水平面所成的锐角为45°．在此过程中，钢管的中点M所走的路径长是________米（结果用无理数表示）．

Answer 1

分析：连接OM、OM'，则发现OM始终等于AB的一半，则钢管的中点M所走的路径长为弧OMM'的长度，求出∠MOM'的度数，代入弧长的计算公式即可得出答案．
解答：连接OM、OM'，

∵∠ABO=75°，∠OBM'=45°，
∴∠AOM=∠MAO=15°，∠M'OB=∠M'BO=45°，
∴∠MOM'=90°-15°-45°=30°，
则钢管的中点M所走的路径长=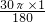=m．
故答案为：．
点评：本题考查了弧长的计算，解答本题的关键是确定点M行走路径，要求同学们熟练记忆弧长的计算公式．