题目内容
 如图,在?ABCD中,AB=8,AD=6,∠DAB=30°,点E,F在AC上,且AE=EF=FC,则△BEF的面积为
如图,在?ABCD中,AB=8,AD=6,∠DAB=30°,点E,F在AC上,且AE=EF=FC,则△BEF的面积为
- A.8
- B.4
- C.6
- D.12
B
分析:可先求平行四边形的总面积,因为AE=EF=FC,所以三个小三角形的面积相等,进而可求解.
解答: 解:如图,过点D作DG⊥AB于点G,
解:如图,过点D作DG⊥AB于点G,
∵AD=6,∠DAB=30°,∴DG=3,
∴平行四边形ABCD的面积为S=AB•DG=8×3=24,
∴△ABC的面积为S= ×24=12
×24=12
∴△BEF的面积S= ×12=4
×12=4
故选B.
点评:平行四边形的面积等于平行四边形的边长与该边上的高的积.即 S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高,并注意体会三角形面积相等的条件.
分析:可先求平行四边形的总面积,因为AE=EF=FC,所以三个小三角形的面积相等,进而可求解.
解答:
 解:如图,过点D作DG⊥AB于点G,
解:如图,过点D作DG⊥AB于点G,∵AD=6,∠DAB=30°,∴DG=3,
∴平行四边形ABCD的面积为S=AB•DG=8×3=24,
∴△ABC的面积为S=
 ×24=12
×24=12∴△BEF的面积S=
 ×12=4
×12=4故选B.
点评:平行四边形的面积等于平行四边形的边长与该边上的高的积.即 S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高,并注意体会三角形面积相等的条件.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=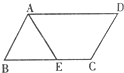 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.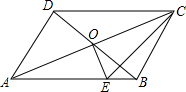 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是