题目内容
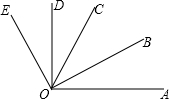 如图,∠AOC=70°,∠COE=40°,OB是∠AOC的平分线,OD是∠COE的平分线.
如图,∠AOC=70°,∠COE=40°,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)求∠BOD的度数;
(2)若∠AOC=α(α为锐角),其它条件不变,则∠BOD=________;
(3)若∠COE=β(β为锐角),其它条件不变,则∠BOD=________;
(4)若∠AOC=α,∠COE=β(α、β为锐角),则∠BOD=________.
解:(1)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC= ∠AOC=
∠AOC= ×70°=35°,
×70°=35°,
∠COD= ∠COE=
∠COE= ×40°=20°,
×40°=20°,
∴∠BOD=∠BOC+∠COD=35°+20°=55°
答:∠BOD为55°.
(2)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC= ∠AOC=
∠AOC= ×α=
×α= α,
α,
∠COD= ∠COE=
∠COE= ×40°=20°,
×40°=20°,
∴∠BOD=∠BOC+∠COD= α+20°.
α+20°.
故答案为: α+20°.
α+20°.
(3)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC= ∠AOC=
∠AOC= ×70°=35°,
×70°=35°,
∠COD= ∠COE=
∠COE= ×β=
×β= β,
β,
∴∠BOD=∠COD+∠BOC= β+35°.
β+35°.
故答案为: β+35°.
β+35°.
(4)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC= ∠AOC=
∠AOC= ×α=
×α= α,
α,
∠COD= ∠COE=
∠COE= ×β=
×β= β,
β,
∴∠BOD=∠BOC+∠COD= α+
α+ β.
β.
故答案为: α+
α+ β.
β.
分析:根据角平分线定义和已知条件,分别求出∠BOC和∠COD的度数,然后相加即可得出答案,同理可求出(2)(3)(4)的答案.
点评:此题主要考查学生对角的计算的理解和掌握,此题难度不大属于中档题.
∴∠BOC=
 ∠AOC=
∠AOC= ×70°=35°,
×70°=35°,∠COD=
 ∠COE=
∠COE= ×40°=20°,
×40°=20°,∴∠BOD=∠BOC+∠COD=35°+20°=55°
答:∠BOD为55°.
(2)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC=
 ∠AOC=
∠AOC= ×α=
×α= α,
α,∠COD=
 ∠COE=
∠COE= ×40°=20°,
×40°=20°,∴∠BOD=∠BOC+∠COD=
 α+20°.
α+20°.故答案为:
 α+20°.
α+20°.(3)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC=
 ∠AOC=
∠AOC= ×70°=35°,
×70°=35°,∠COD=
 ∠COE=
∠COE= ×β=
×β= β,
β,∴∠BOD=∠COD+∠BOC=
 β+35°.
β+35°.故答案为:
 β+35°.
β+35°.(4)∵OB平分∠AOC,OD平分∠COE,
∴∠BOC=
 ∠AOC=
∠AOC= ×α=
×α= α,
α,∠COD=
 ∠COE=
∠COE= ×β=
×β= β,
β,∴∠BOD=∠BOC+∠COD=
 α+
α+ β.
β.故答案为:
 α+
α+ β.
β.分析:根据角平分线定义和已知条件,分别求出∠BOC和∠COD的度数,然后相加即可得出答案,同理可求出(2)(3)(4)的答案.
点评:此题主要考查学生对角的计算的理解和掌握,此题难度不大属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 23、下面是马小虎解的一道题:
23、下面是马小虎解的一道题: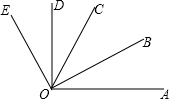 如图,∠AOC=70°,∠COE=40°,OB是∠AOC的平分线,OD是∠COE的平分线.
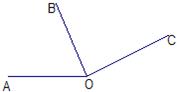
如图,∠AOC=70°,∠COE=40°,OB是∠AOC的平分线,OD是∠COE的平分线. 如图,∠AOB=70°,射线OC是可绕点O旋转的动射线,当∠BOC=15°时,则∠AOC的度数是( )
如图,∠AOB=70°,射线OC是可绕点O旋转的动射线,当∠BOC=15°时,则∠AOC的度数是( )