题目内容
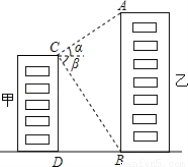
(10分)如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30°,测得乙楼底部B点的俯角β为60°,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
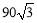 ;
; .
.
【解析】
试题分析:作CE⊥AB于点E,在Rt△ACE和Rt△BCE中,利用tanβ=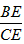 ,和tanα=
,和tanα= ,可求出BE、AE的长,然后可解决问题.
,可求出BE、AE的长,然后可解决问题.
试题解析:作CE⊥AB于点E,

∵CE∥DB,CD∥AB,且∠CDB=90°,
∴四边形BECD是矩形,
∴CD=BE,CE=BD,
在Rt△BCE中,β=60°,CE=BD=90米,
∵tanβ=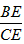 ,
,
∴BE=CE·tanβ=90×tan60°=90 (米),
(米),
∴CD=BE=90 (米),
(米),
在Rt△ACE中,α=30°,CE=90米,
∵tanα= ,
,
∴AE=CE·tanα=90×tan30°=90×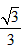 =30
=30 (米),
(米),
∴AB=AE+BE=30 +90
+90 =120
=120 (米),
(米),
答:甲楼高为90 米,乙楼高为120
米,乙楼高为120 米.
米.
考点:解直角三角形的应用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
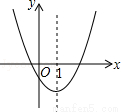

 的顶点坐标是( )
的顶点坐标是( ) B.
B.  C.
C.  D.
D.