Question

如图，在扇形EAB中，半径长AB=10，∠EAB=90°；以AB为直径作半圆O，点D是弧BE上的一个动点，BD与半圆O交于点C，DG⊥AB于点G，DG与AC交于点F，连结OF．
（1）求证：DC=BC；
（2）设AG=x，FG²=y，试求y关于x的函数关系式，并写出x的取值范围；
（3）若点G落在线段OB上，当△FOG∽△ABC时，求线段AG的长度．

Answer 1

（1）证明：如图，连接AD．
∵点D、B在弧BE上，
∴AD=AB．
∵点C在半圆O上，AB为半圆O的直径，
∴∠ACB=90°，即AC⊥BD，
∴DC=BC；

（2）∵AD=AB=10，AG=x，
∴BG=10-x．
∵DG⊥AB于点G，
∴在直角△ADG中，DG²=AD²-AG²=100-x²，
∴DG=．
∵∠CAB+∠B=∠D+∠B=90°，
∴∠FAG=∠D，
∴Rt△AFG∽Rt△DBG，
∴=，
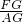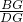∴=，则FG=，
∴y=FG²=，期中，x的取值范围为：0≤x≤10；

（3）在点D运动过程中，若点G落在线段OB上，且△FOG∽△ABC时．
∵Rt△AFG∽Rt△ABC，
∴Rt△FOG∽Rt△AFG，
∴FG²=AG•OG=x（x-5），
∴=x（x-5），
解得：x=，
经检验可知，AG=．
综上所述，当△FOG∽△ABC时，AG=．
分析：（1）如图，连接AD，构建等腰△ABD，理由等腰三角形的“三线合一”的性质证得结论；
（2）在直角△ADG中，由勾股定理得到：DG²=AD²-AG²=100-x²，则易求DG=；然后通过相似三角形Rt△AFG∽Rt△DBG的对应边成比例知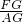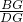：=，即
=，易求y=FG²=，期中，x的取值范围为：0≤x≤10；
（3）在点D运动过程中，若点G落在线段OB上，且△FOG∽△ABC时．结合Rt△AFG∽Rt△ABC，推知Rt△FOG∽Rt△AFG，则该相似三角形的对应边成比例：
FG²=AG•OG=x（x-5），解得：x=，经检验可知，AG=．
点评：本题综合考查了圆周角定理，等腰三角形的性质，勾股定理以及相似三角形的判定与性质．难度较大，需要学生对所学知识有一个系统的，综合性的掌握．