Question

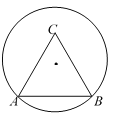
【题目】如图，正△ABC的边长为2，点A、B在半径为的圆上，点C在圆内，将正△ABC绕点A逆时针旋转，当点C第一次落在圆上时，旋转角的正切值是_______________.

Answer 1

【答案】

【解析】分析：

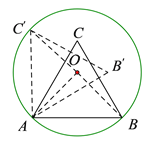
如下图，连接OA、OB、OC′，由已知条件易证△AOB和△AOC′都是等腰直角三角形，从而可得∠BAC′=90°，结合∠BAC=60°可得∠CAC′=30°，由此可得旋转角为30°，从而可得旋转角的正切值为.

详解：

如下图，连接OA、OB、OC′，

由题意可得：OA=OB=OC′=，AB=AC′=2，

∵，

∴△AOB和△AOC′都是等腰直角三角形，

∴∠OAB=∠OAC′=45°，

∴∠BAC′=90°，

又∵∠BAC=60°，

∴旋转角∠CAC′=30°，

∴tan∠CAC′=.

故答案为.