题目内容
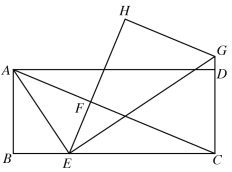
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是对角线,点
是对角线,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,点
上,点![]() 在射线
在射线![]() 上,连接
上,连接![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 所在直线,则线段
所在直线,则线段![]() 的长度为( )
的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
利用勾股定理可求出AC=13,设BE=x,则EC=12-x,根据折叠的性质可得EF=BE=x,CF=13-5=8,再次利用勾股定理建立方程求出x,得到BE的长,然后求AE,最后利用△ABE∽△ECG建立比例式可求出EG.
在Rt△ABC中,
AC=![]()
设BE=x,则EC=12-x,
由折叠的性质可得∠AFE=∠B=90°,AF=AB=5,EF=BE=x,则CF=AC-AF=13-5=8
在Rt△CEF中,![]()
即![]() ,解得
,解得![]()
∴AE=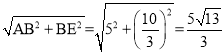 ,EC=BC-BE=
,EC=BC-BE=![]()
由折叠的性质可得∠AEB=∠AEF,∠GEH=∠GEC
∴∠AEB+∠GEC=![]()
∵∠AEB+∠BAE=90°
∴∠BAE=∠GEC,
又∵∠B=∠GCE=90°
∴△ABE∽△ECG
∴![]() ,即
,即
∴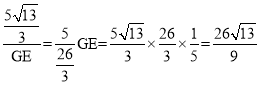
故选:B.

练习册系列答案
相关题目
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.